Maxxon
- 4
- 0
I'd like to calculate how much torque a hollow cylinder along its axis can take before it will start to buckle. The cylinder is held at one end, and the torque is applied equally in discrete intervals along the length of the cylinder.
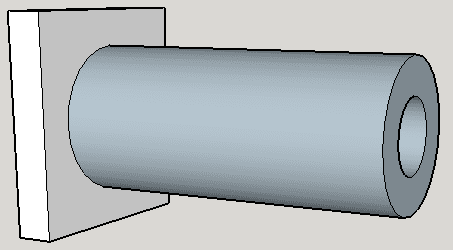
In the example image above, the hollow cylinder is mounted on a slab which is immovable.
I'm guessing I need to know the tensile strength of the material the hollow cylinder is made of, the thickness of the cylinder wall and the diameter of the cylinder. Is that correct?
Is there a formula that I can use to calculate this information?
In the example image above, the hollow cylinder is mounted on a slab which is immovable.
I'm guessing I need to know the tensile strength of the material the hollow cylinder is made of, the thickness of the cylinder wall and the diameter of the cylinder. Is that correct?
Is there a formula that I can use to calculate this information?