How to determine the number of turns of the winding?

[Leonid92]

Homework Statement

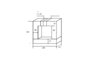
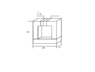
In the core made of electrical steel (Fig. 1), it is required to create a magnetic flux Φ = 4.2*10^(-3) Wb. Determine the number of turns of the winding, if the current is I = 5 A, and the dimensions of the core are specified in millimeters.

Relevant Equations

Φ = B*S
I*w = H*L

1) B = Φ/S = (4.2*10^(-3) Wb)/(2.5*10^(-3) m^2) = 1.68 T
2) Using electrical steel magnetization curve given in the textbook: magnetic field strength H corresponding to magnetic flux density 1.68 T is equal to 6000 A/m.
3) L is a length of the middle magnetic line of the core (Fig. 2).
L = 2*(200 - 50 + 200 - 50) = 600 mm = 0.6 m
4) According to Kirchhoff's second law for a magnetic circuit:
I*w = H*L,
where w is a number of turns of the winding.
Then:
w = (H*L)/I = 720.

Is it right solution?

The problem is that true answer given in the textbook is w = 240.

Could you please advise good reference book where one can find electrical steel magnetization curve? I'd like to check H value in another book.

 

[rude man]

If H is given as 6000 A/m then you don't need any B information. No permeability, no B flux - just the dimensions of the core: Hd = NI where d is path distance (Ampere's law).

 

[Leonid92]

If H is given as 6000 A/m then you don't need any B information. No permeability, no B flux - just the dimensions of the core: Hd = NI where d is path distance (Ampere's law).

Thank you for reply!
When posting the thread, I made a mistake. Actually, H is not given. One should determine H using calculated B value and electrical steel magnetization curve.

 

[rude man]

Thank you for reply!
When posting the thread, I made a mistake. Actually, H is not given. One should determine H using calculated B value and electrical steel magnetization curve.

Makes more sense!
So determine B then divide by mu.
You need to use your textbook magnetization data or you'll get the wrong answer. There are many different kinds of steel, even "electrical steel" (never heard that term before), each with its unique data.

 

[Tom.G]

"electrical steel" (never heard that term before)

It's a term sometimes used to refer to Silicon Steel, typically as used in transformer laminations.