Tom31415926535
- 9
- 0
Homework Statement
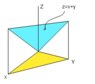
Let G be the region bounded by the planes x=0,y=0,z=0,x+y=1and z=x+y.
Homework Equations
(a) Find the volume of G by integration.
(b) If the region is a solid of uniform density, use triple integration to find its center of mass.
The Attempt at a Solution
[/B]
My understanding is that I need to setup a triple integral:
∫∫∫dxdydz
I’m just a little unsure about how to determine the terminals