- #1
ostrogradsky
- 8
- 0
Must double integrate using type I or type II planar region D to find volume bounded by
Cylinder y^2+z^2=4
And
Planes
X=2y
X=0
Z=0
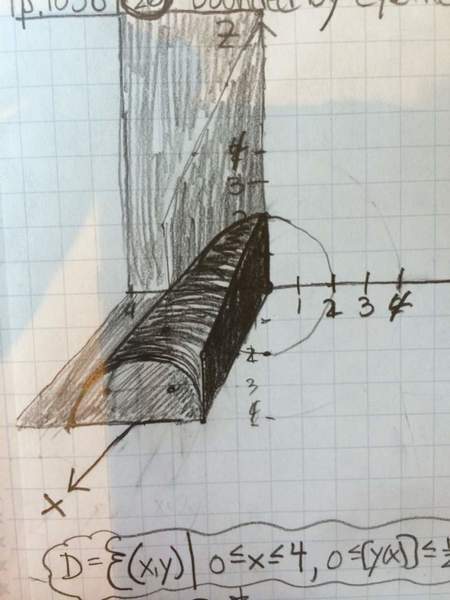
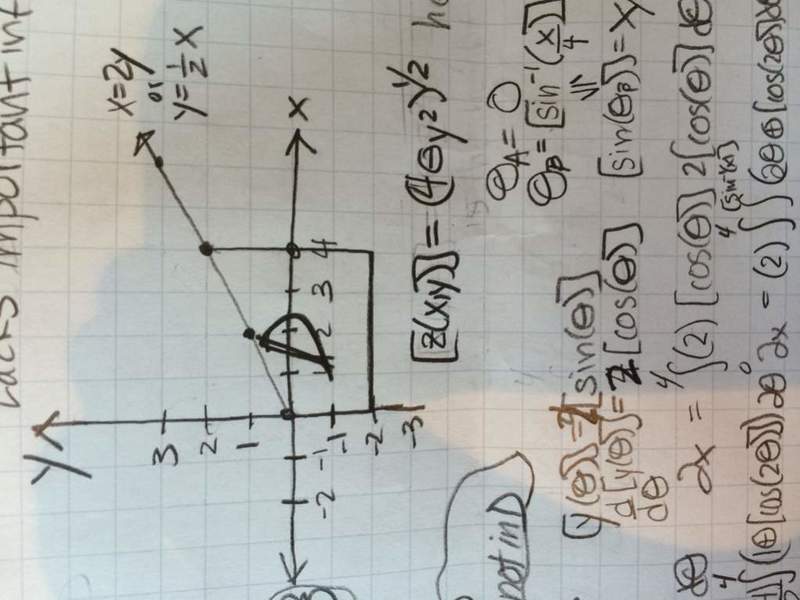
Cylinder y^2+z^2=4
And
Planes
X=2y
X=0
Z=0
You have totally ignored the comments about this image being sideways.ostrogradsky said:You're going to have to look at picture to even make sense of the scribbles I wrote above. So no more complaints.
ostrogradsky said:
The formula for finding the volume of a shape bounded by a cylinder and planes is V = πr²h, where r is the radius of the base of the cylinder and h is the height of the cylinder.
To calculate the volume when the shape is bounded by multiple planes, we need to find the volume of each individual shape and then subtract the overlapping areas. For example, if a cylinder is bounded by two planes, we would find the volume of the cylinder and then subtract the volume of the overlapping section.
No, the volume bounded by a cylinder and planes cannot be negative. It is a measure of physical space and therefore cannot have a negative value.
The positions and orientations of the planes can greatly affect the volume bounded by a cylinder. If the planes are parallel to the base of the cylinder, the volume will be the same as the volume of a cylinder. However, if the planes are at an angle or intersect the cylinder, the volume will be different and will need to be calculated using the formula for finding the volume of a shape bounded by multiple planes.
Yes, it is possible for the volume bounded by a cylinder and planes to be greater than the volume of the cylinder itself. This can happen if the planes intersect the cylinder in a way that creates additional space within the boundaries of the shape.