How to find acceleration of 2 masses on a pulley on slanted plane

[infinitylord]

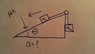
---see attachment for picture of problem---
There is no actual numbers given. We are supposed to be solving for acceleration and I tried but can't find an answer. I'll show you my work and please tell me what I did wrong

Ʃfx= Ff + T - w1sinθ = m1ax = 0
Ʃfy= N - wcosθ = m1ay
Ʃfx= 0 = m2ax = 0
Ʃfy = T - w2 = m2ay
Ff = μN --- w2 = m2g

then I began to plus stuff in
T = m2g + m2ay or T = m2(g + ay)
μN + m2g + m2ay - w1sinθ = 0

then I tried to solve for normal force and got
N = (w1sinθ - m2g +m2ay)/μ

I then tried to plug N into [N - w1cosθ = -m1ay]
(w1sinθ - m2g +m2ay)/μ - w1cosθ = -m1ay

I tried to solve from there for acceleration
w1sinθ - m2g + m2ay = -m1ay + w1cosθ * μ ----
w1sinθ + ay = (-m1ay + w1cosθ + m2gμ)/m2
a = -m1ay + w1cosθ + gμ - w1sinθ

obviously acceleration cancels out my way and that means I can't solve. So any help on how to do this problem would be greatly appreciated

 

[Spinnor]

Study the last worked example in,

http://www.ux1.eiu.edu/~cfadd/1150-05/06Applications/atwoods.html

Found via,

https://www.google.com/search?q=fin...O40gGeyYCgBw&ved=0CAQQ_AUoAA&biw=1093&bih=491

 

[haruspex]

Ʃfx= Ff + T - w1sinθ = m1ax = 0
Ʃfy= N - wcosθ = m1ay
Ʃfx= 0 = m2ax = 0
Ʃfy = T - w2 = m2ay
Ff = μN --- w2 = m2g

It's difficult to pinpoint the error without an actual definition for each of the variables. In fact, failure to lay out such a definition in advance is often the source of the error.
Clearly you have chosen different co-ordinate systems for the two masses, and that's fine. But the constancy of string length gives you an equation relating an acceleration of one to an acceleration of the other. What is that equation?
(You have the wrong acceleration equated to zero for m1. Maybe that's just a typo in the post and is not propagated in later working - I haven't checked.)