How to find beam spring stiffness coefficient?

AI Thread Summary
To find the beam spring stiffness coefficient, the total stiffness can be calculated using Ktotal = F/Δtotal, with Δtotal defined as ½(Δ1 + Δ2) for a mass at mid-span. The assumption that K1 equals K2 leads to Ktotal being the sum of K1 and K2, indicating no flexibility in the beam. However, the discussion highlights that the parallel springs formula may not apply since the springs displace differently to maintain equilibrium. A unique formula may be necessary to accurately reflect this behavior. The conversation emphasizes the need for careful consideration of spring displacement in beam stiffness calculations.
cognosco123
Messages
1
Reaction score
0
The problem is attached.
2015-09-13 22.58.08.jpg
 
Engineering news on Phys.org
I think you can solve it generally using the relationships:
Ktotal =F/Δtotal
Δtotal = ½(Δ1 + Δ2)

assuming the mass is located at mid-span.
 
Last edited:
The statement "If K1 = K2, Ktotal = K1 + K2" implies that there is no flexibility in the beam. The post title suggest that you want the stiffness to reflect the stiffness of the beam as well. Which is it?
 
Daniel Sadlier said:
The equivalent spring constant Ktot = k1 + k2 no matter the values of k1 or k2.
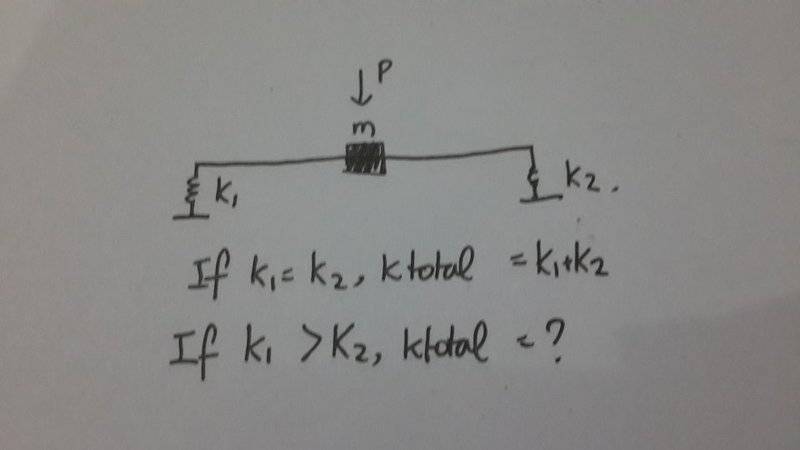
I'll disagree on this. The parallel springs formula assumes that both springs displace the same. Here, however, the springs will displace differently to maintain equilibrium. Therefore, a unique formula needs to be derived.
 

Thread 'Bubble formation in 4 mm gap vessel'

How did you find PF?: Via Google search Hi, I have a vessel I 3D printed to investigate single bubble rise. The vessel has a 4 mm gap separated by acrylic panels. This is essentially my viewing chamber where I can record the bubble motion. The vessel is open to atmosphere. The bubble generation mechanism is composed of a syringe pump and glass capillary tube (Internal Diameter of 0.45 mm). I connect a 1/4” air line hose from the syringe to the capillary The bubble is formed at the tip...
View full post »
Thread 'Physics of Stretch: What pressure does a band apply on a cylinder?'

Thread 'Physics of Stretch: What pressure does a band apply on a cylinder?'

Scenario 1 (figure 1) A continuous loop of elastic material is stretched around two metal bars. The top bar is attached to a load cell that reads force. The lower bar can be moved downwards to stretch the elastic material. The lower bar is moved downwards until the two bars are 1190mm apart, stretching the elastic material. The bars are 5mm thick, so the total internal loop length is 1200mm (1190mm + 5mm + 5mm). At this level of stretch, the load cell reads 45N tensile force. Key numbers...
View full post »

Thread 'Find 3D Printer & Software Resources for Prototype Creation'

I'd like to create a thread with links to 3-D Printer resources, including printers and software package suggestions. My motivations are selfish, as I have a 3-D printed project that I'm working on, and I'd like to buy a simple printer and use low cost software to make the first prototype. There are some previous threads about 3-D printing like this: https://www.physicsforums.com/threads/are-3d-printers-easy-to-use-yet.917489/ but none that address the overall topic (unless I've missed...
View full post »

Similar threads

Automotive Calculation of the reduced stiffness of a simple suspension
Replies
3
Views
2K
How to calculate the stiffness of a spring wire cantilever beam?
Replies
4
Views
2K
What is the best resource for information on mechanical springs?
Replies
6
Views
5K
Simply supported beam with a spring support in the middle - deflection
Replies
6
Views
3K
How to solve spring mass damper system manually?
Replies
16
Views
3K
Variable pitch spring calculations
Replies
1
Views
2K
Stiffness by pressure calculations
Replies
9
Views
2K
Increasing Cantilever Beam Stiffness
Replies
7
Views
5K
Vibration and Modal Analysis: Adding massless springs to a shaft
Replies
6
Views
2K
Why are stiff springs more responsive?
Replies
23
Views
10K

Hot Threads

Recent Insights

Back
Top