You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
How to Find Co-ordinates on a Diagram for Simulating Tides?
- Thread starter lektor
- Start date
-
- Tags
- Random
AI Thread Summary
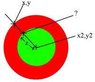
To find coordinates on a diagram lacking a coordinate system, establishing a reference frame with defined x and y axes is essential. Without this, coordinates can only be determined relative to known points, such as (X2,Y2) as an origin. By defining a principal direction towards another point (X,Y), a unit vector can be created to express the unknown point marked with a "?". The radius of the inner circle, denoted as Z, is also necessary for accurate calculations. This discussion highlights the importance of a coordinate system for simulating tides effectively.
Physics news on Phys.org
HallsofIvy
Science Advisor
Homework Helper
- 42,895
- 984
Actually, no, because there is no coordinate system!
Do you intend to have a coordinate system with x and y axes horizontal and vertical?
Assuming that and that you are given coordinates (x,y) and (x2,y2) you can find the slope and equation of the line between them but you would still need to know the radius of the inner circle to find the coordinates of the point marked with a "?".
Do you intend to have a coordinate system with x and y axes horizontal and vertical?
Assuming that and that you are given coordinates (x,y) and (x2,y2) you can find the slope and equation of the line between them but you would still need to know the radius of the inner circle to find the coordinates of the point marked with a "?".
BobG
Science Advisor
- 352
- 88
Without a reference frame, you can't find the coordinates. However, you can find the coordinates relative to X2,Y2 and X,Y.lektor said:Hey can someone tell me how to find the co-ordinates on this diagram.
If you let X2,Y2 be your origin, you can define your principal direction as being directed towards X,Y. Whether you create a unit vector in this direction or use some other length vector in this direction to define your reference, ? will just be some scalar multiple of your reference vector.
In other words, you can set it up so that if the value of X, Y, X2, Y2, and Z were later given, the coordinates of ? would naturally follow.
Last edited:
lektor
- 56
- 0
Hey in reply to the first post Z is the radius of the inner circle, and this was for a friend who is trying to make a program to simulate the tides.
I picked up this problem from the Schaum's series book titled "College Mathematics" by Ayres/Schmidt. It is a solved problem in the book. But what surprised me was that the solution to this problem was given in one line without any explanation. I could, therefore, not understand how the given one-line solution was reached.
The one-line solution in the book says: The equation is ##x \cos{\omega} +y \sin{\omega} - 5 = 0##, ##\omega## being the parameter.
From my side, the only thing I could...
Similar threads
- Replies
- 2
- Views
- 1K
- Replies
- 10
- Views
- 5K
- Replies
- 4
- Views
- 1K
- Replies
- 16
- Views
- 2K
- Replies
- 1
- Views
- 1K
- Replies
- 3
- Views
- 2K
- Replies
- 3
- Views
- 3K
- Replies
- 4
- Views
- 16K
- Replies
- 7
- Views
- 1K
- Replies
- 2
- Views
- 2K
Hot Threads
-
Geometry: Similar Shapes
- Started by paulb203
- Replies: 116
- Precalculus Mathematics Homework Help
-
Length of Diagonal
- Started by erobz
- Replies: 45
- Precalculus Mathematics Homework Help
-
Approximate value of ##E=1/2! +1/3!+1/4!+... ##
- Started by littlemathquark
- Replies: 12
- Precalculus Mathematics Homework Help
-
Find integer points on this equation
- Started by littlemathquark
- Replies: 8
- Precalculus Mathematics Homework Help
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math