liucibegemoc
- 9
- 0
Hello.
I have an electric circuit that's made from conductors, resistors and coils.
I needed to find a voltage between two points and I did. Got answer that plot is:
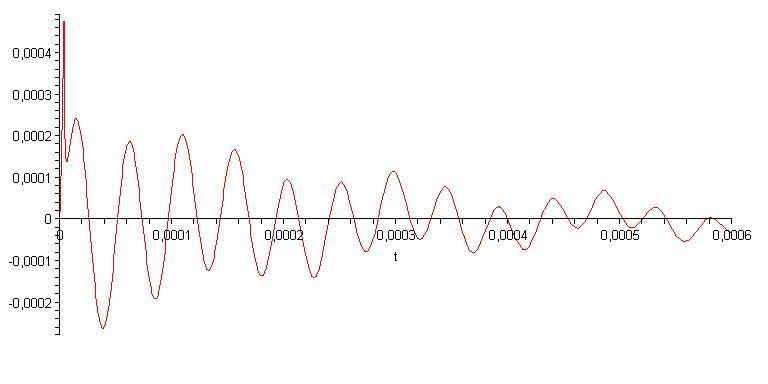
I need to find electric circuit parameters like resonance, degression constant and other.
My teacher said something about finding zeros of current equation denominator.
Sorry for my English, but I'm in trouble. Please help me.
I have an electric circuit that's made from conductors, resistors and coils.
I needed to find a voltage between two points and I did. Got answer that plot is:
I need to find electric circuit parameters like resonance, degression constant and other.
My teacher said something about finding zeros of current equation denominator.
Sorry for my English, but I'm in trouble. Please help me.