SHENGTON
- 6
- 0
Hello guys!
I need your help regarding Projectile Motion because I kinda novice here. I don't know where to start.
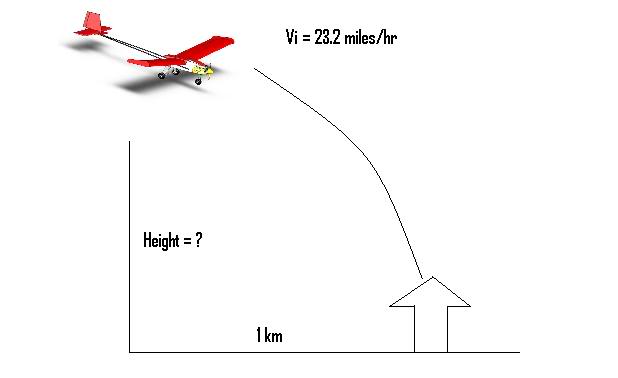
These are the following given:
Vi = 23.2 miles/hour
h = ?
x = 1 km
Here's the situation it looks like, check this image that I created for you to understand.
Hope someone can help me with this.
Thanks and God bless. :)
I need your help regarding Projectile Motion because I kinda novice here. I don't know where to start.
These are the following given:
Vi = 23.2 miles/hour
h = ?
x = 1 km
Here's the situation it looks like, check this image that I created for you to understand.
Hope someone can help me with this.
Thanks and God bless. :)