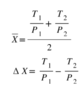How to find the change from a differentials problem (thermal)

[Clara Chung]

How to get from 14.24 to 14.25?

 

[Charles Link]

To me it looks like they got the signs wrong. $\\$ $\Delta S_2=(\frac{1}{T_2}) \Delta U+ (\frac{p_2}{T_2}) \Delta V$. $\\$ Meanwhile $\Delta S_1=- [(\frac{1}{T_1})\Delta U+(\frac{p_1}{T_1}) \Delta V ]$. $\\$ Then $\Delta S _{system} =\Delta S_1+\Delta S_2$ $\\$ @Chestermiller Did I get the sign wrong, or did the book get the sign wrong?

 

[Chestermiller]

To me it looks like they got the signs wrong. $\\$ $\Delta S_2=(\frac{1}{T_2}) \Delta U+ (\frac{p_2}{T_2}) \Delta V$. $\\$ Meanwhile $\Delta S_1=- [(\frac{1}{T_1})\Delta U+(\frac{p_1}{T_1}) \Delta V ]$. $\\$ Then $\Delta S _{system} =\Delta S_1+\Delta S_2$ $\\$ @Chestermiller Did I get the sign wrong, or did the book get the sign wrong?

What is it supposed to mean for internal energy to be transferred from system 1 to system 2? Internal energy is supposed to be a physical property of a material, not a quantity of energy in transit? Do they mean heat rather than internal energy? I have major problems with this question statement. This is the kind of thing that confuses students to no end.

Chet

 

[Charles Link]

What is it supposed to mean for internal energy to be transferred from system 1 to system 2? Internal energy is supposed to be a physical property of a material, not a quantity of energy in transit? Do they mean heat rather than internal energy? I have major problems with this question statement. This is the kind of thing that confuses students to no end.

Chet

What I think you are saying, @Chestermiller is even if a quantity of heat $\Delta Q$ goes from system 1 to system 2, there is no guarantee that it goes into the $\Delta U$ term=it could also go into the $p \Delta V$ term, so the problem really lacks definition. Did I understand your comments accurately?

 

[Chestermiller]

I think what the question meant to analyze was a case where you have two systems in contact with one another having different temperatures and pressures, but with a constant total volume and a constant total internal energy. The combined system is insulated and rigid on the outside. The barrier between the chambers is released and allowed to move freely, and the system is then allowed to re-equilibrate. The idea is to determine the change in entropy from the initial to the final state, and to show that the only way entropy doesn't increase is that if the initial temperatures and the initial pressures match. For ideal gases, this problem can be analyzed without too much trouble. But I strongly disagree with using Eqn. 14-24 to analyze this because that equation applies only to closely neighboring equilibrium states of a system, and the equilibrium states would not be closely neighboring for each of the two chambers involved.

If the OP would like to analyze the ideal gas problem I described, I would be glad to help.

 

[Chestermiller]

Clara, Is your "like" an indication that you would like me to help you solve this problem correctly (rather than the way your book does it)?

 

[Clara Chung]

Clara, Is your "like" an indication that you would like me to help you solve this problem correctly (rather than the way your book does it)?

Dear Chestermiller,
I am thinking about it

 

[Clara Chung]

But I strongly disagree with using Eqn. 14-24 to analyze this because that equation applies only to closely neighboring equilibrium states of a system, and the equilibrium states would not be closely neighboring for each of the two chambers involved.

I don't understand why the equation only applies to closely neighboring equilibrium states, could you explain a bit more?

 

[George Jones]

I don't understand why the equation only applies to closely neighboring equilibrium states

Are you familiar (as covered in something like Calc 3) with the Taylor expansion about $\left( x_0 , y_0 \right)$ of a function of two variables, $f \left( x , y \right)$?

 

[Chestermiller]

I don't understand why the equation only applies to closely neighboring equilibrium states, could you explain a bit more?

The thermodynamic functions U and S apply only to thermodynamic equilibrium states.

 

[Clara Chung]

Are you familiar (as covered in something like Calc 3) with the Taylor expansion about $\left( x_0 , y_0 \right)$ of a function of two variables, $f \left( x , y \right)$?

Yes, f(x,y) = f(x₀, y₀) + ∂f/∂x (x-x₀) + ∂f/∂y (y-y0) + error term, but what are the function and variables?

 

[Clara Chung]

I think what the question meant to analyze was a case where you have two systems in contact with one another having different temperatures and pressures, but with a constant total volume and a constant total internal energy. The combined system is insulated and rigid on the outside. The barrier between the chambers is released and allowed to move freely, and the system is then allowed to re-equilibrate. The idea is to determine the change in entropy from the initial to the final state, and to show that the only way entropy doesn't increase is that if the initial temperatures and the initial pressures match. For ideal gases, this problem can be analyzed without too much trouble. But I strongly disagree with using Eqn. 14-24 to analyze this because that equation applies only to closely neighboring equilibrium states of a system, and the equilibrium states would not be closely neighboring for each of the two chambers involved.

If the OP would like to analyze the ideal gas problem I described, I would be glad to help.

If I use solve it as an ideal gas, let the system with T₁ , P₁, V₁ and n₁ be system 1.
Let the system with T₂ , P₂, V₂ and n₂ be system 2.
Let the final temperature be T_f and final pressure be P_f.
I try to find the change of entropy between two equilibrium states, so if change in entropy = 0, the two equilibrium states will be equivalent?(I am not sure about this statement.
The internal energy of the system 1 and system 2 remains the same, i.e. n₁ T₁ + n₂ T₂ = (n₁ + n₂ )T_f.
Consider system 1,
the first reversible step will be an isothermal expansion from V₁ to V₁ + V₂,
the entropy change in this reversible process is n₁ R ln (V₁ + V₂ / V₁).
the second step will be an isochoric heating to slowly increase the temperature from T₁ to T_f,
dQrev = C_v dT
ΔS₁=C_v ln (T_f / T₁) + n₁ R ln (V₁ + V₂ /V₁)

Similarly for system 2,
so the total change in entropy is:
ΔS₁ + ΔS₂
= C_v ln (T_f / T₁) + n₁ R ln ((V₁ + V₂) /V₁) + C_v ln (T_f / T₂) + n₂ R ln ((V₁ + V₂) /V₂)

Then I don't know how to preceed with the volume term...

 

[Clara Chung]

Sorry I have another question... Is entropy an unique property? Is there two different equilibrium states with different values of entropy? For example... Energy is a state function... but it is ok for two different equilibrium states to have the same temperature (but with different volume/ pressure) etc...

 

[Chestermiller]

If I use solve it as an ideal gas, let the system with T₁ , P₁, V₁ and n₁ be system 1.
Let the system with T₂ , P₂, V₂ and n₂ be system 2.
Let the final temperature be T_f and final pressure be P_f.
I try to find the change of entropy between two equilibrium states, so if change in entropy = 0, the two equilibrium states will be equivalent?(I am not sure about this statement.
The internal energy of the system 1 and system 2 remains the same, i.e. n₁ T₁ + n₂ T₂ = (n₁ + n₂ )T_f.
Consider system 1,
the first reversible step will be an isothermal expansion from V₁ to V₁ + V₂,
the entropy change in this reversible process is n₁ R ln (V₁ + V₂ / V₁).
the second step will be an isochoric heating to slowly increase the temperature from T₁ to T_f,
dQrev = C_v dT
ΔS₁=C_v ln (T_f / T₁) + n₁ R ln (V₁ + V₂ /V₁)

Similarly for system 2,
so the total change in entropy is:
ΔS₁ + ΔS₂
= C_v ln (T_f / T₁) + n₁ R ln ((V₁ + V₂) /V₁) + C_v ln (T_f / T₂) + n₂ R ln ((V₁ + V₂) /V₂)

Then I don't know how to preceed with the volume term...

Very nice job, but the problem is a little over-specified and there should be n's in front of the Cv's. You need to use the ideal gas law for the initial conditions to express V1 and V2 in terms of P1, T1, n1 and P2, T2, n2. Also, if there is a sliding barrier present between the two gases, the final volume of each gas is not equal to the total volume of the container. For one of the gases, its volume increases, and, for the other gas, its volume decreases by an equal amount. The change in volume of each is determined by requiring that the final pressure is the same for each. So, with these comments, please go back and determine the final pressure.

 

[Chestermiller]

Sorry I have another question... Is entropy an unique property?

Yes. It is a physical property of the material.

Is there two different equilibrium states with different values of entropy? For example... Energy is a state function... but it is ok for two different equilibrium states to have the same temperature (but with different volume/ pressure) etc...

Sure. You already showed that for an ideal gas, where the entropy is a function of temperature and specific volume (or, equivalently, temperature and pressure)

 

[Clara Chung]

Very nice job, but the problem is a little over-specified and there should be n's in front of the Cv's. You need to use the ideal gas law for the initial conditions to express V1 and V2 in terms of P1, T1, n1 and P2, T2, n2. Also, if there is a sliding barrier present between the two gases, the final volume of each gas is not equal to the total volume of the container. For one of the gases, its volume increases, and, for the other gas, its volume decreases by an equal amount. The change in volume of each is determined by requiring that the final pressure is the same for each. So, with these comments, please go back and determine the final pressure.

P1 V1 = n1 R T1
P2 V2 = n2 R T2
Pf (V1+V2) = (n1 + n2) R Tf
so Pf = (n1 + n2) R Tf / (V1+V2)
The new volume of system 1 will be
V1_f= n1 R Tf / [(n1 + n2) R Tf / (V1+V2)]
= (V1+V2) n1 / (n1+n2)
Similarly for system 2 the change in volume will be
V2_f= n2 R Tf / [(n1 + n2) R Tf / (V1+V2)]
= (V1+V2) n2 / (n1+n2)
It is quite surprising that the volume each gas occupied is not the same as the total volume...
Should I proceed in the calculation of change in entropy with these results? However, the calculation will be so complicated because n1 and n2 will contribute as power in the logarithm...?

 

[Clara Chung]

Yes. It is a physical property of the material.

Sure. You already showed that for an ideal gas, where the entropy is a function of temperature and specific volume (or, equivalently, temperature and pressure)

So, if I have 2 systems, each with the same value of entropy, however the temperature of system A is higher than the temperature in system B, will there be a heat transfer from system A to system B?
Mathematically, entropy is a function of T and V, i.e. S(T,V), is it possible that
S(T1 , V1) = S(T2, V2) for different temperature and volume? (This would imply two system are not in equilibrium even if ΔS=0 between the two systems)
or
S depends only on temperature?

 

[Chestermiller]

Eliminate V1 and V2 using the initial conditions to express Pf exclusively in terms of T1, T2, P1, P2, n1, and n2. Then calculate entropy change of each gas from $$\Delta S=nC_p\Delta (\ln{T})-nR\Delta (\ln{P})$$

 

[Chestermiller]

So, if I have 2 systems, each with the same value of entropy, however the temperature of system A is higher than the temperature in system B, will there be a heat transfer from system A to system B?

Sure.

Mathematically, entropy is a function of T and V, i.e. S(T,V), is it possible that
S(T1 , V1) = S(T2, V2) for different temperature and volume? (This would imply two system are not in equilibrium even if ΔS=0 between the two systems)
or
S depends only on temperature?

Let's see how it plays out when we do what I just said in my previous post.

 

[Chestermiller]

To simplify things (temporarily), let's just, for now, focus on the case where n1=n2=1

 

[Clara Chung]

OK.

??

 

[Chestermiller]

OK.

View attachment 236704
??

What happened to the n2 chamber?

 

[Clara Chung]

What happened to the n2 chamber?

If my equation is correct, the total change in entropy for n1=n2=1 will be

??

 

[Chestermiller]

If my equation is correct, the total change in entropy for n1=n2=1 will be
View attachment 236705
??

If I multiply and divide the expression in brackets of the 2nd term in your relationship by $T_1T_2$, I obtain:
$$\Delta S=C_p\ln{\left(\frac{(T_1+T_2)^2}{T_1T_2}\right)}-R\ln{\left(\frac{(T_1+T_2)^2}{T_1T_2}\frac{\left(\frac{T_1}{P_1}\right)\left(\frac{T_2}{P_2}\right)}{\left(\frac{T_1}{P_1}+\frac{T_2}{P_2}\right)^2}\right)}$$This can be rewritten as:
$$\Delta S=C_v\ln{\left(\frac{(T_1+T_2)^2}{T_1T_2}\right)}+R\ln{\left(\frac{\left(\frac{T_1}{P_1}+\frac{T_2}{P_2}\right)^2}{\left(\frac{T_1}{P_1}\right)\left(\frac{T_2}{P_2}\right)}\right)}$$
OK so far? Note the similarity in mathematical form for the two logarithmic terms. I will continue after you indicate you are comfortable with these results.

 

[Clara Chung]

If I multiply and divide the expression in brackets of the 2nd term in your relationship by $T_1T_2$, I obtain:
$$\Delta S=C_p\ln{\left(\frac{(T_1+T_2)^2}{T_1T_2}\right)}-R\ln{\left(\frac{(T_1+T_2)^2}{T_1T_2}\frac{\left(\frac{T_1}{P_1}\right)\left(\frac{T_2}{P_2}\right)}{\left(\frac{T_1}{P_1}+\frac{T_2}{P_2}\right)^2}\right)}$$This can be rewritten as:
$$\Delta S=C_v\ln{\left(\frac{(T_1+T_2)^2}{T_1T_2}\right)}+R\ln{\left(\frac{\left(\frac{T_1}{P_1}+\frac{T_2}{P_2}\right)^2}{\left(\frac{T_1}{P_1}\right)\left(\frac{T_2}{P_2}\right)}\right)}$$
OK so far? Note the similarity in mathematical form for the two logarithmic terms. I will continue after you indicate you are comfortable with these results.

OK. I am comfortable with the result

 

[Chestermiller]

We are missing a factor of 4 in the denominator of each of the logarithmic terms. For example, for the first term, the final temperature is $(T_1+T_2)/2$

I can write $$T_1T_2=\left(\frac{(T_1+T_2)}{2}\right)^2-\left(\frac{(T_1-T_2)}{2}\right)^2$$ so $$\frac{(T_1+T_2)^2}{4T_1T_2}=\frac{1}{\left[1-\frac{1}{4}\left(\frac{\Delta T}{\bar{T}}\right)^2\right]}$$ where $\bar{T}=\frac{(T_1+T_2)}{2}$and $\Delta T=(T_1-T_2)$. This expression is >1 for all values $\Delta T\neq 0$, which means it always makes a positive contribution to the entropy change.

What does the same procedure tell you for the second term in the entropy change equation.

 

[Clara Chung]

We are missing a factor of 4 in the denominator of each of the logarithmic terms. For example, for the first term, the final temperature is $(T_1+T_2)/2$

I can write $$T_1T_2=\left(\frac{(T_1+T_2)}{2}\right)^2-\left(\frac{(T_1-T_2)}{2}\right)^2$$ so $$\frac{(T_1+T_2)^2}{4T_1T_2}=\frac{1}{\left[1-\frac{1}{4}\left(\frac{\Delta T}{\bar{T}}\right)^2\right]}$$ where $\bar{T}=\frac{(T_1+T_2)}{2}$and $\Delta T=(T_1-T_2)$. This expression is >1 for all values $\Delta T\neq 0$, which means it always makes a positive contribution to the entropy change.

What does the same procedure tell you for the second term in the entropy change equation.

And the same expression with T bar and ΔT replaced by X bar and ΔX. 2 X bar is always larger than ΔX, so the contribution to entropy is always positive. The change in entropy is zero when ΔT=0 and ΔX=0

 

[Clara Chung]

Therefore the entropy change is zero if and if only the temperature and pressure are equal between two equilibrium states. Does it mean if two states have the same value of entropy, the two states are identical? (States with different temperature but the same entropy don't exist?)

 

[Chestermiller]

Therefore the entropy change is zero if and if only the temperature and pressure are equal between two equilibrium states. Does it mean if two states have the same value of entropy, the two states are identical? (States with different temperature but the same entropy don't exist?)

No. It only means that, at equilibrium, entropy is a minimum with respect to changes in the intensive variables.