- #1
uyger
- 4
- 0
How can I find the radius of a circle by knowing two points and its arc length? Do I have to use a numerical method to solve for a trigonometric equation or is there any algebraic or geometric method?
JHamm said:Orient the two points to lie on the horizontal (just makes description easier) and draw a line between them. The part of the arc that lies above halfway along this line is now a third point, draw a line vertically down from this point. Now draw a third line from one of your two original points to the new one drawn on the arc, the angle this new line makes with the vertical is the angle a fourth (and final) line needs to be drawn at from the other end of your newest line towards the vertical one to form an isosceles triangle with the two equal length sides being the radii.
Attached is an image which I'm sure will be easier to follow
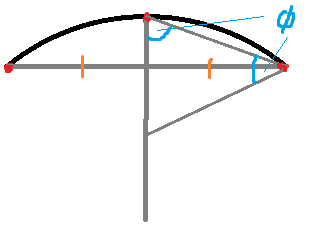
Thank you for the reply but as you did not use the length of the arc it is impossible to reach a solution by your way. Actually there are number of mistakes but I am sure you can notice them at a second glance. Again thank you for your effort.JHamm said:Orient the two points to lie on the horizontal (just makes description easier) and draw a line between them. The part of the arc that lies above halfway along this line is now a third point, draw a line vertically down from this point. Now draw a third line from one of your two original points to the new one drawn on the arc, the angle this new line makes with the vertical is the angle a fourth (and final) line needs to be drawn at from the other end of your newest line towards the vertical one to form an isosceles triangle with the two equal length sides being the radii.
Attached is an image which I'm sure will be easier to follow
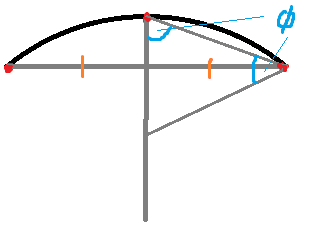
DivisionByZro said:If by the radii you mean the two segments marked with the orange lines, then no, that's not the radius. You can't just assume that the segment of arc that you picked forms half the circle.
I was thinking if you could find the curvature of the circle somehow, then you'd be done. This is a problem seeing as finding the curvature of any curve usually require you to know at least parametric equations of the curve. Do you have any more information regarding these two points, are they arbitrarily spread out on the circle?
DivisionByZro said:So just to clear things up, by "two points known" you mean the coordinates are known? And the arc length is the length of the arc contained between the two points correct? (There are actually two ways to see this, any two points on a circle cut the circle into two parts of possibly different arc lengths). In either case, I don't think you can find the radius of the circle with the given information (at least not that I see right away). I'll keep thinking about it.
D H said:This problem is not solvable by elementary methods. You are inevitably going to end up with a transcendental expression.
It is easily solvable by approximation techniques.
DivisionByZro said:If by the radii you mean the two segments marked with the orange lines, then no, that's not the radius. You can't just assume that the segment of arc that you picked forms half the circle.
uyger said:Thank you for the reply but as you did not use the length of the arc it is impossible to reach a solution by your way.
Nonsense.JHamm said:No, the two angles marked [itex]\phi[/itex] form the base of an isosceles triangle who's equal sides are the radius, the two lines marked with orange lines are just of equal length.
D H said:Nonsense.
Try your technique with an arc length of 14.1897054604163922812851617102553083 and the two points being the origin and (14,0). There's no room in that picture for the radius of the circle (which happens to be 25 in this example).
Maybe you didn't.JHamm said:Maybe I didn't explain well enough
To find the radius of a circle using two points and its arc length, you can use the formula: r = (arc length * 2) / (distance between two points). The distance between the two points can be calculated using the distance formula: d = √((x2-x1)^2 + (y2-y1)^2). Once you have the radius, you can use it to find the circumference or area of the circle.
Yes, as long as the two points are not on the same diameter of the circle. If the two points are on the same diameter, the distance between them will be equal to the diameter, making it impossible to find the radius using this method.
If you only know the coordinates of the two points, you can still use the same formula mentioned above to find the radius of the circle. Make sure to use the coordinates to calculate the distance between the two points before plugging it into the formula.
No, in order to find the radius of a circle using this method, you need to know the coordinates of the two points. If you only know the arc length, you will need to use a different method to find the radius, such as using the central angle and arc length relationship.
Yes, you can draw a triangle using the two points and the center of the circle. The length of one of the sides of the triangle would be the radius of the circle. You can then use the Pythagorean theorem to solve for the radius. Alternatively, you can also use a compass to construct the circle using the two points and measure the radius directly from the compass.