nineeyes
- 21
- 0
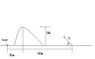
Problem : find a v_i and angle \theta that will be able to hit the target 795 m away and clear the 60 m hill 600 m away. I attached a picture of the problem.
I was trying to do this using the equation
y=y_0+(x-x_0)*tan(\theta)-\frac {1}{2}g (\frac {x-x_0}{v_0*cos(\theta)})^2
I used this by seperating the problem into two parts from the origin to x=600 m and y=60m (y_0 = x_0 = 0) and the second part from x= 795 m and y=0 m(y_0=60m , x_0=600m)
I know this is wrong, because I couldn't get an answer. I was wondering what the best way to approach this problem would be. Thanks in advance!
I was trying to do this using the equation
y=y_0+(x-x_0)*tan(\theta)-\frac {1}{2}g (\frac {x-x_0}{v_0*cos(\theta)})^2
I used this by seperating the problem into two parts from the origin to x=600 m and y=60m (y_0 = x_0 = 0) and the second part from x= 795 m and y=0 m(y_0=60m , x_0=600m)
I know this is wrong, because I couldn't get an answer. I was wondering what the best way to approach this problem would be. Thanks in advance!
Attachments
Last edited: