OFF_Smog
- 3
- 0
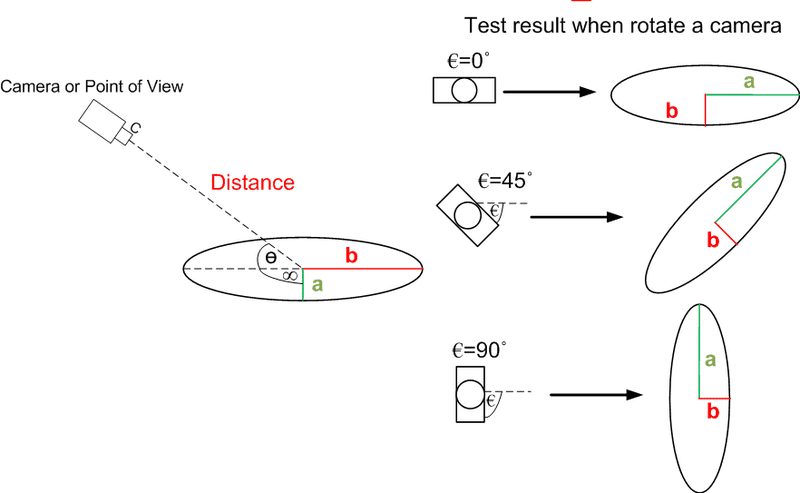
As we know a circle view at an angle appears as an ellipse ,
as you see in the picture, the center of the camera aim to the center of the circle ,
the angle between the circle axis and the camera is ө,
the azimuth between mojor axis(a) and the camera is ∞,
the rotation of the camera is €,
1. How to predict an orientation of major and minor axis and the ratio of its axes(b/a) ,if we only know these ө,∞,€ angle, regardless of size of ellipses
2. Is there any theory to apply this example?
as you see in the picture, the center of the camera aim to the center of the circle ,
the angle between the circle axis and the camera is ө,
the azimuth between mojor axis(a) and the camera is ∞,
the rotation of the camera is €,
1. How to predict an orientation of major and minor axis and the ratio of its axes(b/a) ,if we only know these ө,∞,€ angle, regardless of size of ellipses
2. Is there any theory to apply this example?