How to read a Gamma Ray Spectrum

[krizam]

For some of my work, I am investigating methods of scanning for nuclear material. As part of my study, I have run across Gamma Ray Spectroscopy: http://en.wikipedia.org/wiki/Gamma_spectroscopy"

What I am having trouble with is reading a gamma ray spectrum (I am a software engineer with a limited physics background).

I have two examples that are confusing me (from that wikipedia article):

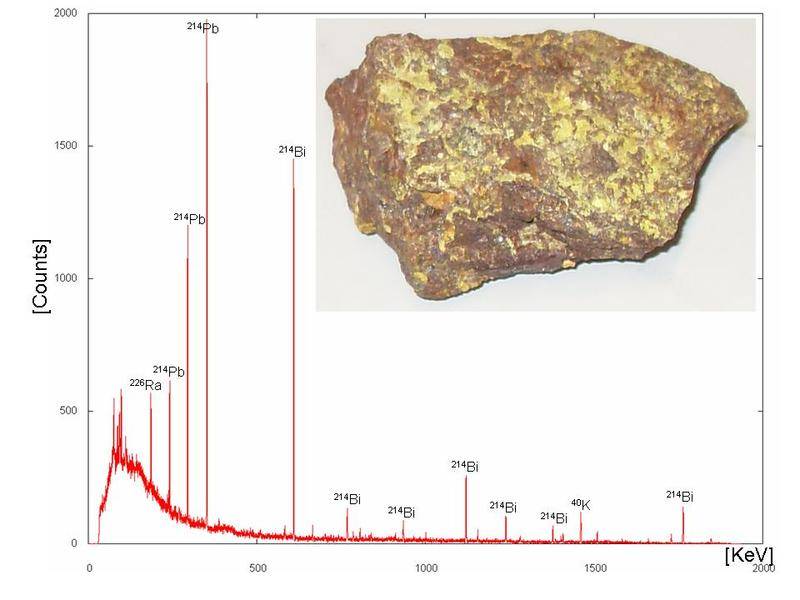
What do the axes actually mean? I get the concept of the "count" being the activity of the detector. What are the peaks showing? Do peaks at certain spots signify a "fingerprint" for an isotope (Such as 214 BI having 7 peaks?)?

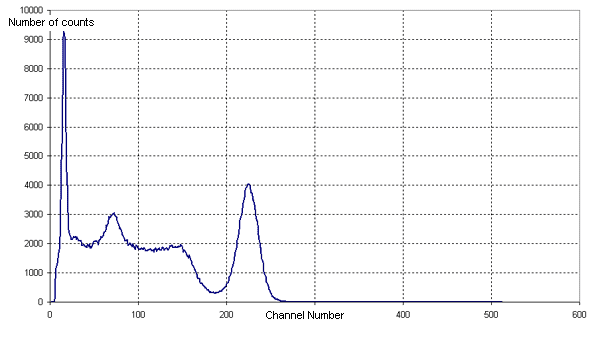
Why is the bottom axis on this graph labeled as "channel number"? How is that different then the previous graph? In the article it says for this figure that "An example of a NaI spectrum is the gamma spectrum of the cesium isotope 137Cs—see Figure XXX. 137Cs emits a single gamma line of 662 keV." Is this represented somehow in this figure?


Thanks for any help. I just am looking for a basic understanding so I can read these spectrums.

 

[ansgar]

you have to calibrate the channel numbers so that they correspond to energy.

each nucleus has its energy leves, just as atoms, which can be populated and de.-excited.
(this you should know from high school)

 

[diditgi]

It is simpler than you expect, probably :-).

On the Y axis there are number of events (number of photons which have hit the detector).

The X axis is proportional to the energy of the events, usually translates via
calibration to keV.
The "channel number" on the X axis refers to the raw ADC conversion result from
each event, usually 0 to 8191 (sometimes to 4095 or to 16383) for HPGe detectors
and within 1023 or even less for NaI.
Calibration channel number -> energy may be nonlinear (it is that for NaI while
it is linear for HPGe), so normally an MCA will allow you to enter multiple calibration
points and will maintain the respective polynomial.

------------------
http://tgi-sci.com
------------------