robijnix
- 3
- 0
1. how do i solve
X'(t)=A(t)X(t)
I know of this equation:
x(t) = x_0 \exp\left( \int_{t_0}^t f(\xi) \, d\xi \right)
but i think that I'm using it wrong.
i have the following mathematica code:
A=
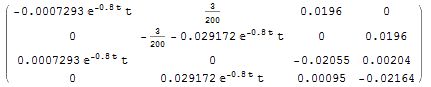
x = MatrixExp[Integrate[A, {t, 0, s}]].{1, 0,0,0};
Plot[x[[2]] + x[[4]], {s, 0, 500}]
the problem is, that the result i get it not the same as when i numerically plot it with matlab, which leads me to believe that I'm doing something wrong.
any kind of help would be greatly appreciated,
Thanks
X'(t)=A(t)X(t)
Homework Equations
I know of this equation:
x(t) = x_0 \exp\left( \int_{t_0}^t f(\xi) \, d\xi \right)
but i think that I'm using it wrong.
The Attempt at a Solution
i have the following mathematica code:
A=
x = MatrixExp[Integrate[A, {t, 0, s}]].{1, 0,0,0};
Plot[x[[2]] + x[[4]], {s, 0, 500}]
the problem is, that the result i get it not the same as when i numerically plot it with matlab, which leads me to believe that I'm doing something wrong.
any kind of help would be greatly appreciated,
Thanks
Last edited: