BernieCooke
- 5
- 0
Homework Statement
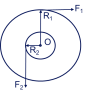
So I generally understand how to solve the following problem. My only roadblock is that I am not sure I am solving the moment of Inertia correctly. I know that for a solid cylinder you would use I = 1/2mr^2, but I am not sure how if it has only one mass given of 10 kg, yet the rod has a thicker radius at one point than another, you would solve for I. Any help would be greatly appreciated.A solid cylinder of mass 10 kg is pivoted about a frictionless axis through its center O. A rope wrapped around the outer radius R1 = 1.0 m, exerts a force of F1 = 5.0 N to the right. A second rope wrapped around another section of radius R2 = 0.50 m exerts a force of F2 = 6.0 N downward.
What is the angular acceleration of the disk?
If the disk starts from rest, how many radians does it rotate through in the first 5.0 s?
Homework Equations
torque = force x moment arm
torque = moment of inertia x angular acceleration
moment of inertia for a solid cylinder = 1/2 mass x radius squared
The Attempt at a Solution
I = 1/2 (10)(1)^2 for the first section of cylinder which gives 5 for moment of inertia
I = 1/2 (10)(.5)^2 for the section section which gives 1.25 for moment of inertia
combined = 6.25