- #1
requied
- 98
- 3
- Homework Statement
- Evaluate the integral below
- Relevant Equations
- there is no equations(?)
I have a question like this;
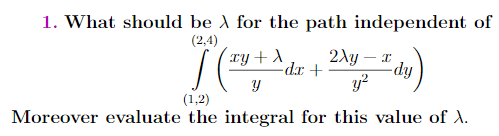
I selected lambda as 4 (I actually don't know what it must be) and try to make clear to myself like
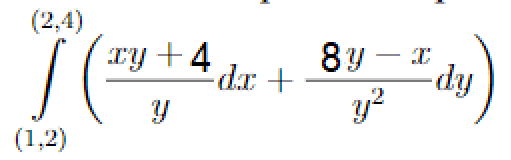
these limits (1,2) and (2,4) is x and y locations I think :)
If I find an answer for part one of the integral following, I would apply this on another:
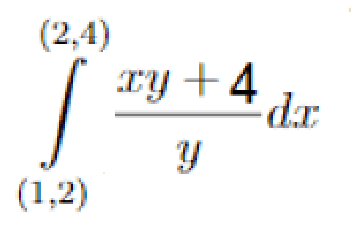
My solution was :
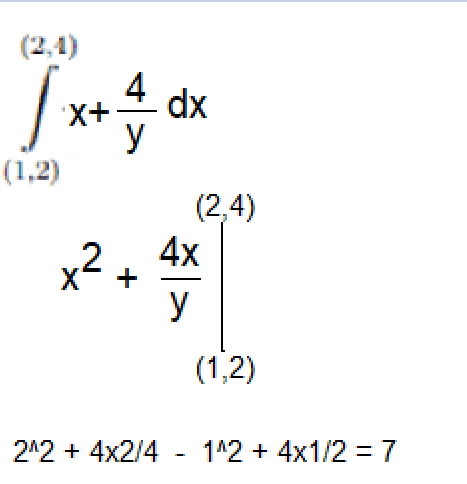
I wonder whether it is correct. If it is not, how must I imagine?
Note: If there is someone who has an idea about original question, please leave a comment. I appreciate it :)
I selected lambda as 4 (I actually don't know what it must be) and try to make clear to myself like
these limits (1,2) and (2,4) is x and y locations I think :)
If I find an answer for part one of the integral following, I would apply this on another:
My solution was :
I wonder whether it is correct. If it is not, how must I imagine?
Note: If there is someone who has an idea about original question, please leave a comment. I appreciate it :)