Helly123
- 581
- 20
Homework Statement
Homework Equations
The Attempt at a Solution
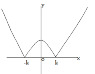
I think the answer for number 1 , graph somewhat like this
I get trouble for 2, 3, etc
I (k) = ##\int_{-1}^{1} f(x) dx ##
f(x) = ## \mid x^2 - k^2 \mid##
2) k < 1
for negative side
##\int_{-1}^{-k} (x^2 - k^2) dx + \int_{-k}^{0} (k^2 - x^2) dx ##
## \frac{x^3}{3} - k^2 {\mid} _{-1}^{-k} + (k^2 - \frac{x^3}{3} {\mid} )_{-k}^{0} ##
## \frac{-k^3}{3} - k^2 - (\frac{-1}{3} - k^2) + k^2 - (k^2 - \frac{-k^3}{3} ) ##
## \frac{1}{3} - \frac{2k^3}{3} ##
for positive side
##\int_{0}^{k} (k^2 - x^2) dx + \int_{k}^{1} ( x^2 - k^2 ) dx ##
## k^2 - \frac{k^3}{3} - k^2 + \frac{1}{3} - k^2 - (\frac{k^3}{3} - k^2) ##
## \frac{1}{3} - \frac{2k^2}{3} ##
total = ## - \frac{4k^3}{3} + \frac{2}{3} ##
but it is wrong.. why?total = ## - \frac{4k^3}{3} + \frac{2}{3} ##
3) k > 1
for negative side
##\int_{-1}^{0} (k^2 - x^2) dx + \int_{0}^{1} (k^2 - x^2) dx ##
but I get zero.
but I get zero.