How to solve this without resorting to inertial forces

[arestes]

Homework Statement

I have been solving problems on my own and I came out with a problem I made up myself.
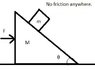
It's simple: There's a triangular big block of mass M with an angle of $\theta$ and on top of it there's a rectangular block of mass m. See figure attached.
When the triangular block is acted upon a horizontal force F, both will accelerate (I can, without loss of generality, assume the big block accelerates to the right). I just wanted to find the acceleration of each block with respect to the ground, which is frictionless and so is the interface between the blocks.

Homework Equations

[itex]\sum \vec{F} = m \vec{a}<br /> <br /> <h2>The Attempt at a Solution</h2><br /> Ok, reposting here as this looks too much like a h/w problem, although it's not :D<br /> <br /> I managed to solve the problem first isolating the triangular block and finding the horizontal acceleration. It was crucial to use the constraint of motion along the ground only. Likewise, When I go to the non inertial frame of reference of the accelerating block to analyze the FBD of the smaller block, I use the constraint of motion along the incline. From there, I can find the magnitude of the normal force between the blocks BUT also using the inertial *fictitious* force that needs to be considered for using a non inertial frame of reference. 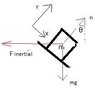THIS IS WHAT BOTHERS ME.<br /> <br /> Calling "n" the normal force between the blocks, and "$n_g$ the normal force between the ground and the big block, the FBD of the triangular block gives me <br /> $\sum F_x = F-n Sin(\theta) = M a_M$<br /> $\sum F_y = n_g-Mg-n Cos(\theta) = 0$<br /> The FBD of the small block *once I hop onto the non inertial frame of reference of the accelerating incline* gives me *see figure*<br /> $\sum F_x = mg Sin(\theta) - F_{inert}Cos(\theta) = m a_m$<br /> $\sum F_y = n-mgCos(\theta)- F_{inert}Sin(\theta) = 0$<br /> <br /> <br /> The last equation is the constraint I needed, but I use the inertial force with magnitude $F_{inert} = \frac{m(F-nSin(\theta) )}{M}= m a_M$. Solving these equation is enough to find the value of n and from there, just plug it back into $a_M$, but I don't like this<br /> From here, I can totally solve the problem (I already got the answer, which relied crucially on finding n, and I have 4 unknowns and 4 equations, I already did it).<br /> <br /> **** I would like to work entirely with inertial frames of reference.*****<br /> I was used to always work with an inertial frame of reference (like the ground), even when I had rotating bodies. In the latter case I could use the constraint that the centripetal force must be equal to $\frac{m\cdot v^2}{R}$. However, in the problem I'm talking about, the constraint is not clear from the frame of reference of the ground. I need to figure out a constraint to solve for the normal foce.<br /> Any thoughts of how I can avoid the non inertial frame of reference?[/itex]

 

[WannabeNewton]

The constraint is just that the block has to remain tangential to the wedge while the wedge accelerates. Use geometry to write down an explicit equation for this constraint that you can then differentiate to obtain a constraint on the accelerations of the block and wedge.

You can compare with what I did here if you want (similar problem although easier because there is no external force-just a reaction force): https://www.physicsforums.com/showthread.php?t=663865

 

[arestes]

Thanks! It's exactly what I was suspecting:
Although, your simpler problem (with no F) still uses a non inertial frame of reference, and I wanted to avoid that, I managed to find the constraint... I just had to reverse-engineer it because I already found the answer with the other method...and found something plausible... even intuitive... after you think about it! The constraint is
$a_y = -tan(\theta) (a_x-a_M)$
where $a_x$ and $a_y$ are the accelerations of the little block with respect to the desired inertial frame of the ground (horizontal and vertical to it).

BY THE WAY*** what book were you referring to in the problem you posted in that link?? can you please tell me?
thanks

 

[WannabeNewton]

Yep that's the constraint. Nice work :)! You can also derive it geometrically by setting up coordinates attached to some fixed wall and assigning position vectors from the wall to the moving wedge and block and using trigonometry. The book I was referring to is the following: https://www.amazon.com/dp/0521876222/?tag=pfamazon01-20