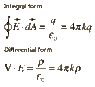PrideofPhilly
- 37
- 0
Homework Statement
A long, thin, straight wire of length L has a positive charge Q distributed uniformly along it. Use Gauss' Law to show that the electric field created by this wire at a radial distance r has a magnitude of E = λ/(2πεor), where λ = Q/L. (Hint: For a Gaussian surface, use a cylinder aligned with its axis along the wire and now that the cylinder has a flat surface at either end, as well as a curved surface.
Homework Equations
The Attempt at a Solution
I have no idea where to start! Please give me a push.