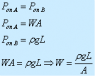HW about presure and wight I need your consulting

[sky08]

Homework Statement

a U-tube with cross-sectional area A and partially filled with oil of density S. A solid cylinder, which fits the tube tightly but can slide without friction, is placed in the right arm. The system is in equilibrium. Find the weight of the cylinder in terms of g, h, A, L, and S.

Homework Equations

I'm using these relationship ;where F is the force of the wight (F=W) & h is hight
P=F/A=W/A
delta(P) = S*g*delta(h)

The Attempt at a Solution

look at my solving and also the figure of question in attachment and tell me what is the wrong in my steps ? why h doesn't appears in the last result?
and thank you very much for your helping before

 

[sky08]

point A and point B I take them in same level where A under the cylinder directly and B in versus side
>>
Hi misters; anybody can help me, please

 

[LowlyPion]

point A and point B I take them in same level where A under the cylinder directly and B in versus side

To be in equilibrium won't the weight of the cylinder equal the weight of the volume of water of height L on the other side?

Volume is Area times L on the left. Density of water is p.
So isn't that simply W = pgAL

 

[sky08]

To be in equilibrium won't the weight of the cylinder equal the weight of the volume of water of height L on the other side?

Volume is Area times L on the left. Density of water is p.
So isn't that simply W = pgAL

why (h) doesn't appears in the last result?

yah I understand you ..
but your result or the weight of cylinder should be depend on all the variables as the Q.

[Find the weight of the cylinder in terms of g, h, A, L, and S.(S or p is density)]
pleas can you explain >>>

thank you Mr.LowlyPion

 

[LowlyPion]

why (h) doesn't appears in the last result?

I took that to mean to express the answer in the unknowns given by the drawing. The answer by inspection of the drawing looks to be independent of h.

Think of it this way. What property of the weight of the cylinder has anything to do with h? L on the other hand defines the volume of oil required to be displaced to hold the cylinder in equilibrium. (You remember Archimedes don't you?)

In your solution you used area in the wrong manner on the weight. It's the weight of the cylinder divided by A that establishes pressure.

What you can say about h is that the solution is only valid for h greater than the diameter of the tube - A/2pi*U²

 

[sky08]

yah that is clearly ... thank you Mr.LowlyPion for your helping
there are small thing also , from where you find this A/2pi*U^2 (U?) ?