Hydraulic Piston Supporting a 500lb weight

Click For Summary
SUMMARY

The discussion focuses on calculating the force vector F required to support a 500 lb weight using two hydraulic pistons with diameters of 0.31 in. and 1.7 in. The participants utilized the equation F1/A1 = F2/A2 to find the force on the first piston but initially misinterpreted the problem by not considering the torque involved. The correct approach involves understanding the relationship between force and distance from the pivot point, leading to the conclusion that the ratio of forces corresponds to the ratio of their distances from the pivot.

PREREQUISITES
  • Understanding of hydraulic systems and Pascal's principle
  • Familiarity with basic physics concepts such as force, area, and torque
  • Knowledge of the formula for calculating area of a circle
  • Ability to manipulate equations involving ratios and proportions
NEXT STEPS
  • Study the principles of Pascal's law in fluid mechanics
  • Learn about torque calculations and their applications in mechanical systems
  • Explore the relationship between force, area, and pressure in hydraulic systems
  • Investigate real-world applications of hydraulic pistons in engineering
USEFUL FOR

Engineering students, mechanical engineers, and anyone interested in understanding hydraulic systems and force calculations in mechanical applications.

AsuraSky
Messages
16
Reaction score
0

Homework Statement



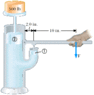
Piston 1 in the figure below has a diameter of 0.31 in.; Piston 2 has a diameter of 1.7 in. In the absence of friction, determine the force vector F necessary to support the 500 lb weight.

p9_24.gif


Homework Equations



F1/A1=F2/A2



The Attempt at a Solution



I used the equation above and found the areas of each piston and solved for F1


F1/.075477=500/2.2698

F1=16.626

That answer was wrong so I thought about it some more and realized that the force I solved for was the force on the piston and not the lever that the question asked for. So I had this crazy idea that since there was sort of a rotational force on the hinge when you push the lever down you can use Torque = rF with torque being the force previously solved for

16.626 = 10(F) (r=10 for the 10 in distance between force F in the diagram and piston 1 in the diagram)

F= 1.6626

This answer was also marked wrong and I have run out of ideas on how to solve this problem. If anyone can point me in the right direction it would be greatly appreciated.
 

Attachments

  • p9_24.gif
    p9_24.gif
    5.3 KB · Views: 730
Physics news on Phys.org
Right method, slight oops.

The ratio of force at the piston and the hand is the ratio of the distances from each of them to the pivot.
 
Thanks, that cleared things up for me.
 

Similar threads

Calculations for Hydraulic Jacks lifting a load
  • · Replies 2 ·
Replies
2
Views
3K
Equilibrium of Forces and Torques on Sawhorses Supporting a Person on a Board
  • · Replies 6 ·
Replies
6
Views
3K
Lifting a car using a hydraulic lift
  • · Replies 3 ·
Replies
3
Views
3K
Plotting the graph of Friction Force vs. time (Laws of motion)
  • · Replies 1 ·
Replies
1
Views
3K
Solve Hydraulic Pump Homework: F1=33.5 N
  • · Replies 1 ·
Replies
1
Views
2K
Piston Question: Have solution, don't understand rationale
  • · Replies 2 ·
Replies
2
Views
8K
Pascal's Principle with Hydraulic Pumps
  • · Replies 21 ·
Replies
21
Views
9K
Expression for pressure in a brake system - is this correct?
  • · Replies 7 ·
Replies
7
Views
2K
Diameter of football player's Piston
  • · Replies 1 ·
Replies
1
Views
5K
Force necessary to support mass on Hydraulic Jack?
  • · Replies 7 ·
Replies
7
Views
7K