birk
- 2
- 0
Hi! First post on this forum, though not the first time visiting :)
I am working on a model of an object falling from one layer of air density into another layer with a higher density, effectively changing the acceleration from positive to negative instantly. (Somehow I am thinking of positive as the downwards direction here). The transition between the two "zones" is instantaneous. (One way to think of it could be an object (that sinks) that falls at a high velocity into water and is abruptly decelerated.)
My question is: How does one calculate the speed of the object after it has entered the new medium? I have seen the following equation for terminal velocity on wikipedia and other sources:
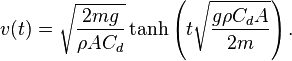
but this assumes an initial velocity of v_0=0
In my situation the initial velocity when entering the new medium is nearly the double of the terminal velocity that I have calculated from the first part:
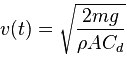
One solution I tried, which I quickly realized how stupid was, was to multiply the function by -1, but this left me with a terminal velocity that increased when the drag coefficient was increased, which is not really what one wants.
Any input would be very much appreciated!
I am working on a model of an object falling from one layer of air density into another layer with a higher density, effectively changing the acceleration from positive to negative instantly. (Somehow I am thinking of positive as the downwards direction here). The transition between the two "zones" is instantaneous. (One way to think of it could be an object (that sinks) that falls at a high velocity into water and is abruptly decelerated.)
My question is: How does one calculate the speed of the object after it has entered the new medium? I have seen the following equation for terminal velocity on wikipedia and other sources:
but this assumes an initial velocity of v_0=0
In my situation the initial velocity when entering the new medium is nearly the double of the terminal velocity that I have calculated from the first part:
One solution I tried, which I quickly realized how stupid was, was to multiply the function by -1, but this left me with a terminal velocity that increased when the drag coefficient was increased, which is not really what one wants.
Any input would be very much appreciated!