- #1
Liam Semeniuk
- 4
- 0
Hi there,
I have never worked with Hypocycloids before so I'm unsure which equations I should be using; but I'll try and get across what I am trying to build. Essentially I am trying to create a series of hypocycloids that act in a similar manner to the "spirograph".
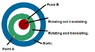
Goal: Three circles set within each other. The outer circle will stay stationary and not rotate. It should be static. The circle set within this circle will rotate along the inner edge of the outer circle and along the outer edge of the innermost circle. The innermost circle should stay stationary, but should rotate as required to accommodate the rotation and drift of the middle circle.
I have attached a diagram (not animated) of what the system should look like.
I have marked two points (Point A and Point B) that should not meet up until the circle has made five rotations around the circle (a total travel of 1800 degrees).
Is it likely that I will need a gear system to implement this?
Any help is appreciated! Thanks!
I have attached a program as well (in C#) that can be used to show what I am aiming for with the outer and middle circle. Set the form to the following:
A = 180
B = 130
C = 130
Fr/Rev = 20
I have never worked with Hypocycloids before so I'm unsure which equations I should be using; but I'll try and get across what I am trying to build. Essentially I am trying to create a series of hypocycloids that act in a similar manner to the "spirograph".
Goal: Three circles set within each other. The outer circle will stay stationary and not rotate. It should be static. The circle set within this circle will rotate along the inner edge of the outer circle and along the outer edge of the innermost circle. The innermost circle should stay stationary, but should rotate as required to accommodate the rotation and drift of the middle circle.
I have attached a diagram (not animated) of what the system should look like.
I have marked two points (Point A and Point B) that should not meet up until the circle has made five rotations around the circle (a total travel of 1800 degrees).
Is it likely that I will need a gear system to implement this?
Any help is appreciated! Thanks!
I have attached a program as well (in C#) that can be used to show what I am aiming for with the outer and middle circle. Set the form to the following:
A = 180
B = 130
C = 130
Fr/Rev = 20
Attachments
Last edited: