Hypodermic Needle Fluid Dynamics

[Adam Quinn]

A hypodermic syringe contains a medicine with the density of water (figure below). The barrel of the syringe has a cross-sectional area of 2.18

10-5 m2. In the absence of a force on the plunger, the pressure everywhere is 1.00 atm.
A force

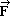of magnitude 1.78 N is exerted on the plunger, making medicine squirt from the needle. Determine the medicine's flow speed through the needle.
Assume the pressure in the needle remains equal to 1.00 atm and that the syringe is horizontal.

I assume the Bernoulli equation is needed
pv1^2/2 + p1 = pv2^2/2 + p2 = constant
pgh would be irrelevant as the needle is horizontal, hence can be removed from both sides of the equation.

So far I have P1 = 101 325 + 1.78/2.18*10^-5 = 182976.38 (2dp)

where do I go from here? Any help would be awesome.

 

[Nidum]

Need the needle bore .

 

[Adam Quinn]

Need the needle bore .

I wasnt given any other measurements, how can I solve for the area of the needle?

 

[Nidum]

Bore of needle is essential to calculate flow rate . If you don't actually know then choose some possible bores and calculate flow for each one to get ball park answers .

You can do it backwards and specify a suitable flow rate and then solve for needle bore if this is easier .

If this is a medical syringe then needle sizes for different purposes are probably available from manufacturers data .

 

[Adam Quinn]

Bore of needle is essential to calculate flow rate . If you don't actually know then choose some possible bores and calculate flow for each one to get ball park answers .

You can do it backwards and specify a suitable flow rate and then solve for needle bore if this is easier .

If this is a medical syringe then needle sizes for different purposes are probably available from manufacturers data .

If it says that the pressure in the needle remains at 1atm, even though liquid is being pushed through, would the force through the first part be equal to the force equal through the needle, and hence p1a1=p2a1?
Would this give me a correct area value?

 

[Nidum]

Is this a real problem to be solved or a study/homework task ?

 

[Adam Quinn]

Is this a real problem to be solved or a study/homework task ?

for study

 

[boneh3ad]

Since they give you all the pressures, you actually don't need the bore of the needle if you make a few simplifying assumptions such as Bernoulli's equation being valid, a constant flow rate, and the syringe being much larger than the needle. In that case, you know everything except for the dynamic pressure in the syringe and can solve for the velocity that way.

 

[Adam Quinn]

Since they give you all the pressures, you actually don't need the bore of the needle if you make a few simplifying assumptions such as Bernoulli's equation being valid, a constant flow rate, and the syringe being much larger than the needle. In that case, you know everything except for the dynamic pressure in the syringe and can solve for the velocity that way.

uh, how? I really don't know...

 

[boneh3ad]

So then let's think about what you do know: baseline pressure in both the needle and syringe (which is equal to atmospheric pressure) and a force applied to a plunger of known cross-sectional area. Is there any way that you can use this information to eliminate all of the other variables from Bernoulli's equation besides the outgoing pressure, particularly in light of the simplifying assumptions I mentioned earlier?

 

[Adam Quinn]

So then let's think about what you do know: baseline pressure in both the needle and syringe (which is equal to atmospheric pressure) and a force applied to a plunger of known cross-sectional area. Is there any way that you can use this information to eliminate all of the other variables from Bernoulli's equation besides the outgoing pressure, particularly in light of the simplifying assumptions I mentioned earlier?

Yes, I have P1, cannot find P2, I can eliminate pgh from both sides of the equation.
I am now left with P1 = 182976.376, A1 = 2.18*10^-5, and the rest of the equation
p1-p2 = 1/2rho (v^2 - v^2)

 

[boneh3ad]

Yes, I have P1, cannot find P2, I can eliminate pgh from both sides of the equation.
I am now left with P1 = 182976.376, A1 = 2.18*10^-5, and the rest of the equation
p1-p2 = 1/2rho (v^2 - v^2)

But you are given $p_2$.

 

[Adam Quinn]

But you are given $p_2$.

p2 doesn't increase from 1atm when the plunger is pushed?

 

[Adam Quinn]

p2 doesn't increase from 1atm when the plunger is pushed?

if not then i have (182976 - 101325)/.5*1000 = v2^2-v1^2

 

[boneh3ad]

p2 doesn't increase from 1atm when the plunger is pushed?

In the problem statement you gave originally, it said to "assume the pressure in the needle remains equal to 1.00 atm and that the syringe is horizontal."

if not then i have (182976 - 101325)/.5*1000 = v2^2-v1^2

The above approximation isn't so great in real life for something as narrow as a needle, but the advantage of something like a narrow needle is that you can make use of another approximation that I mentioned before: namely that the cross section of the syringe is much, much larger than that of the needle.

 

[Adam Quinn]

In the problem statement you gave originally, it said to "assume the pressure in the needle remains equal to 1.00 atm and that the syringe is horizontal."
The above approximation isn't so great in real life for something as narrow as a needle, but the advantage of something like a narrow needle is that you can make use of another approximation that I mentioned before: namely that the cross section of the syringe is much, much larger than that of the needle.

I'm failing to see how this helps me, I can't just say that the cross sectional area of the needle is 0, nor can I say that the velocity is extremely large. (as per a1v1=a2v2, I don't even have a velocity for the tube.)

 

[boneh3ad]

I'm failing to see how this helps me, I can't just say that the cross sectional area of the needle is 0, nor can I say that the velocity is extremely large. (as per a1v1=a2v2, I don't even have a velocity for the tube.)

Ah, but you were almost there. You have just said $v_1 A_1 = v_2 A_2$, with the 1 being the syringe and 2 being the needle. You can safely assume that $A_1 \gg A_2$, so try looking at it in the form
\dfrac{A_2}{A_1} = \dfrac{v_1}{v_2}.

 

[Adam Quinn]

Ah, but you were almost there. You have just said $v_1 A_1 = v_2 A_2$, with the 1 being the syringe and 2 being the needle. You can safely assume that $A_1 \gg A_2$, so try looking at it in the form
\dfrac{A_2}{A_1} = \dfrac{v_1}{v_2}.

hence,
\dfrac{A_1}{2.18*10^{-5}} = \dfrac{v_1}{v_2}
where A1 would be negligible?
hence
\dfrac{v_1}{v_2} = 2.18*10^{-5}

 

[Adam Quinn]

hence,
\dfrac{A_1}{2.18*10^{-5}} = \dfrac{v_1}{v_2}
where A1 would be negligible?
hence
\dfrac{v_1}{v_2} = 2.18*10^{-5}

This could be expressed as
{v_2} = {2.18*10^{-5}}*{v_1}
If this is true then
{182976}-{101325} = {500}*(({2.18*10^{-5}*v_1})-{v_1})

 

[boneh3ad]

This could be expressed as
{v_2} = {2.18*10^{-5}}*{v_1}
If this is true then
{182976}-{101325} = {500}*(({2.18*10^{-5}*v_1})-{v_1})

True, but you are overcomplicating matters. If $A_2/A_1$ is negligibly small, then $v_1/v_2$ must be equally small, and you could say that $v_1 \ll v_2$, which is essentially what you did when you just estimated it as five orders of magnitude smaller (though you had your ratios reversed). For all intents and purposes, then, you could say $v_1 \approx 0$.

 

[Adam Quinn]

This could be expressed as
{v_2} = {2.18*10^{-5}}*{v_1}
If this is true then
{182976}-{101325} = {500}*(({2.18*10^{-5}*v_1})-{v_1})

By solving this I get a negative velocity value, something tells me this means that it's incorrect.

 

[Adam Quinn]

True, but you are overcomplicating matters. If $A_2/A_1$ is negligibly small, then $v_1/v_2$ must be equally small, and you could say that $v_1 \ll v_2$, which is essentially what you did when you just estimated it as five orders of magnitude smaller (though you had your ratios reversed). For all intents and purposes, then, you could say $v_1 \approx 0$.

this would essentially mean that {v_2} = 12.779 m.s^{-1}

 

[Adam Quinn]

this would essentially mean that {v_2} = 12.779 m.s^{-1}

hence
{2.14*10^{-5}}*{v_1}={A_2}*{12.78}

 

[boneh3ad]

By solving this I get a negative velocity value, something tells me this means that it's incorrect.

Right, as I previously pointed out, you mixed up your ratios. It is $v_1$ that should be substantially less than $v_2$, not the other way around.

 

[Adam Quinn]

Right, as I previously pointed out, you mixed up your ratios. It is $v_1$ that should be substantially less than $v_2$, not the other way around.

okay so,
{A_1}{V_1} = {A_2}{V_2}
{A_1} = {2.14*10^{-5}}
\dfrac{A_1}{A_2} = \dfrac{V_2}{V_1}
\dfrac{2.14*10^{-5}}{A_2} = \dfrac{V_2}{V_1}

what do I do from here, please no more riddles, struggling to understand this as it is.

 

[boneh3ad]

okay so,
{A_1}{V_1} = {A_2}{V_2}
{A_1} = {2.14*10^{-5}}
\dfrac{A_1}{A_2} = \dfrac{V_2}{V_1}
\dfrac{2.14*10^{-5}}{A_2} = \dfrac{V_2}{V_1}

what do I do from here, please no more riddles, struggling to understand this as it is.

I am pretty sure I haven't provided any riddles. We discussed that $A_1 \gg A_2$ and how that implies that $v_2 \gg v_1$ and how that implies that you can treat the problem as $v_1 = 0$. I am really not sure how I can be any more straightforward than that short of just doing the problem for you.