Engineering Why Is Current Divided by sqrt(3) in 3-Phase AC Mains?

[thatsmessedup]

Homework Statement

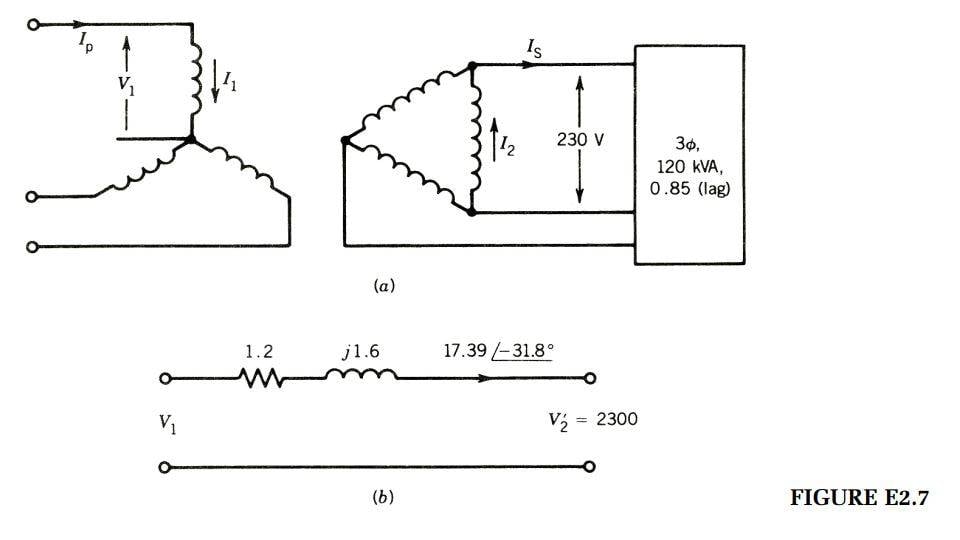
EXAMPLE 2.7
Three 1φ, 50 kVA, 2300=230 V, 60 Hz transformers are connected to form a 3φ, 4000=230 V
transformer bank. The equivalent impedance of each transformer referred to low voltage is
0:012 + j0:016 Ω. The 3φ transformer supplies a 3φ, 120 kVA, 230 V, 0:85 PF (lag) load.
(a) Draw a schematic diagram showing the transformer connection.
(b) Determine the transformer winding currents.
(c) Determine the primary voltage (line-to-line) required.
(d) Determine the voltage regulation

Relevant Equations

Please see attached

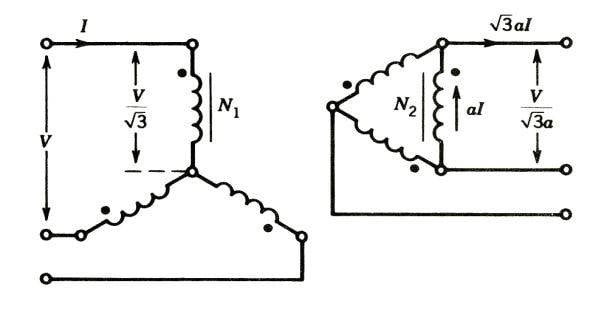
In this example I am thoroughly confused on why Is is divided by sqrt(3). My understanding is that the transformer supplies 3 phase (which is always described in line to line or Y connected). So the current in the winding should be 120[KVA]/230[V] then multiplied by sqrt(3) to convert it to delta line current. Then I2 would be Is divided by sqrt(3) to get the phase current.

Where are the appropiate formulas or diagrams that will make this problem make more sense?
Thanks!

This is where I am seeing that I should multiply sqrt(3) to get the delta line current. (exuding the a because I am not going from one transformer to the other)

 

[NascentOxygen]

If you draw three delta-connected resistances representing the load, in place of that rectangle, and calculate the current in each resistance of that load, it's 120kVA ÷ 3 ÷ 230V

But Is in the diagram is the sum of two of these currents. Is is the line current of a delta-connected load having that value of phase current.

 

[Merlin3189]

In this example I am thoroughly confused on why Is is divided by sqrt(3).

(My understanding is that the transformer supplies 3 phase (which is always described in line to line or Y connected). So the current in the winding should be 120[KVA]/230[V] then multiplied by sqrt(3) to convert it to delta line current. Then I2 would be Is divided by sqrt(3) to get the phase current.)

This is where I am seeing that I should multiply sqrt(3) to get the delta line current. (exuding the a because I am not going from one transformer to the other)
View attachment 257931

The reason is, as you suggest, the same as for the voltages in the primary. If you look at the phase diagrams, you can see the relation.

So, looking only at magnitudes,
$V = V1 \cos {30} + V2 \cos {30} = V1 \sqrt 3 \, \text { or } V1 = \frac {V}{\sqrt3}$
Similarly $I = I1 \cos {30} + I2 \cos {30} = I1 \sqrt 3$