squintyeyes
- 44
- 0
three identical balls are thrown from the same height with the same initial speed...ball a is thrown horizontally, ball b is thrown upward at some angel above the horizontal and ball c is thrown at some angle below the horizontal...disregard air resistance and describe the motions of the three balls and compare the speeds of the balls when they reach the ground.
I think the aswer would go like this however i have reason to believe there is something wrong with this.
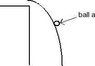
The motion of ball a will resemble an upside down parabola where zero starts at the maximum
pic 1
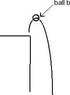
ball b will resemble a parabola as well but it will go up first then down. the reason being that the inital velocity will be counteracted by the acceleration of gravity downwards until the velocity is zero. when the velocity is zero that is the maximum and then the ball b will fall down to earth
pic 2
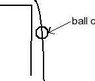
ball c will resemble the downward part of a parabola since it is only going down.
pic 3
in terms of final velocity it will be ball c being fastest, then ball b, then finally ball a being slowest.
the reason for ball c being the fastest is because you are throwing it down at an initial speed while it is being accelerated down at the acceleration of gravity.
the reason that ball b is faster than c is because at ball b's peak and ball c's peak they only have force of gravity in the y direction to speed the ball up. However, ball b is at a higher height so it will have a larger velocity when it hits the ground.
I think the aswer would go like this however i have reason to believe there is something wrong with this.
The motion of ball a will resemble an upside down parabola where zero starts at the maximum
pic 1
ball b will resemble a parabola as well but it will go up first then down. the reason being that the inital velocity will be counteracted by the acceleration of gravity downwards until the velocity is zero. when the velocity is zero that is the maximum and then the ball b will fall down to earth
pic 2
ball c will resemble the downward part of a parabola since it is only going down.
pic 3
in terms of final velocity it will be ball c being fastest, then ball b, then finally ball a being slowest.
the reason for ball c being the fastest is because you are throwing it down at an initial speed while it is being accelerated down at the acceleration of gravity.
the reason that ball b is faster than c is because at ball b's peak and ball c's peak they only have force of gravity in the y direction to speed the ball up. However, ball b is at a higher height so it will have a larger velocity when it hits the ground.