Ideal op amp, difference amplifier?

[Color_of_Cyan]

Homework Statement

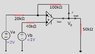
The OP amp in the circuit is ideal. Calculate V₀ if V_a = 2V and V_b = 1V

Homework Equations

V = IR

KCL, KVL,

voltage division, current division,Op-Amp Output V = (Gain)(V+ - V-)(Gain) = -Rf / Rin
Ideal op amp properties:

Input Resistance R_I = ∞

Output Resistance R_o = 0

Gain A = ∞Difference Amplifier:

V_out=(V₂*R_ground(R_f + R₁))/(R₁(R_ground + R₂)) - (R_fV₁/R₁)

The Attempt at a Solution

I still need help understanding op amps, basically. I don't think this is really a differential amplifier but for the formula (and nothing given about any R connected to ground) I think it would simply be

V_out = (-100k/20k)*2V = -10V ?Thank you

 

[CWatters]

Op-amps have very high gain so if they are configured to work as linear amplifiers then V+ must be very close to V-. If they weren't almost identical the output would be driven to one of the supply rails. So in most cases you can assume that V+ = V-

The input impedance of an op-amp is also very high, so in most cases you can assume that the current flowing into the V+ and V- pins is zero. So in your circuit this means:

1) V+ = Vb because there is no current flowing through the 40K.
2) V- = Vb because V- = V+ for linear operation.
3) The current flowing from Va to the V- node must equal that flowing through the 100k feed back resistor.

So based on the above approximations write some equations. For example try applying KCL at the V- node.

After some rearranging you should be able to derive an equation for Vout in terms of Va and Vb.

 

[darkxponent]

Do not just memorise the formulaes. First try to derive it. See the derivation of Vout for difference amplifier in you book and you will find all of what CWatters has said there in the texts. Node analysis and superposition principle are the two things with which you can solve almost any Op-Amp circuit.

 

[Color_of_Cyan]

Op-amps have very high gain so if they are configured to work as linear amplifiers then V+ must be very close to V-. If they weren't almost identical the output would be driven to one of the supply rails. So in most cases you can assume that V+ = V-

The input impedance of an op-amp is also very high, so in most cases you can assume that the current flowing into the V+ and V- pins is zero. So in your circuit this means:

1) V+ = Vb because there is no current flowing through the 40K.
2) V- = Vb because V- = V+ for linear operation.
3) The current flowing from Va to the V- node must equal that flowing through the 100k feed back resistor.

So based on the above approximations write some equations. For example try applying KCL at the V- node.

After some rearranging you should be able to derive an equation for Vout in terms of Va and Vb.

So for the top wire (or the feedback wire?) there is only current because of the big resistance in the op amp?

How do you know what current is coming out of the op amp though?

How do you know what the voltage drop across the 100k is?

Trying what you said though:

2V/20Ω = 1V/(internal resistance) + (V_f/100kΩ)

I = 1V/(internal resistance) = (V_f/100kΩ)


Is there another way to think of an omp amp in terms of another circuit element?

 

[CWatters]

So for the top wire (or the feedback wire?) there is only current because of the big resistance in the op amp?

Apply KCL at the V- node. If there is no current going into or out of the V- pin itself then the current flowing in the 20K and the 100K must be equal.

How do you know what current is coming out of the op amp though?

You don't and it's not relevant.

How do you know what the voltage drop across the 100k is?

What is the voltage on each end? The right hand end is Vout. The left hand end is Vb for the reasons I gave earlier.

Trying what you said though:

2V/20Ω = 1V/(internal resistance) + (V_f/100kΩ)

I = 1V/(internal resistance) = (V_f/100kΩ)

That looks all wrong to me. Try this..

The current flowing in the 20K (left to right assumed to be positive) is

= (Va - V-)/20k
= (Va - Vb)/20k

The current flowing in the 100K is

= (Vb-Vout)/100k

These two currents are equal.

 

[Color_of_Cyan]

That looks more like nodal analysis (something else I need to brush up on again though).

I think I see what you are saying now though.

So

(2V - 1V)/20k = (1V - V_out)/100k

(100k/20k)(2V-1V) = 1V - V_out

5V = 1V - V_out

4V = - V_out

V_out = -4V

I take it that (since) you don't have to worry about any current coming from the output of the op amp then V_out = -V₀ ?

If so

V₀ = 4V.

 

[gneill]

That looks more like nodal analysis (something else I need to brush up on again though).

I think I see what you are saying now though.

So

(2V - 1V)/20k = (1V - V_out)/100k

(100k/20k)(2V-1V) = 1V - V_out

5V = 1V - V_out

4V = - V_out

V_out = -4V

...and... stop right there. V_out is V_o. Don't muck with the sign of the result.

I take it that (since) you don't have to worry about any current coming from the output of the op amp then V_out = -V₀ ?

If so

V₀ = 4V.

No, There will be plenty of current coming out of the op-amp's output; it supplies current to the load as well as to the feedback path. It's just that, for this problem, you're not particularly interested in the total current that the op-amp is driving via its output. You're concerned with finding the potential at the output pin, and for that you need the current traversing the feedback path.

 

[CWatters]

What gneil said. From the diagram Vo is the same sign as the output of the op-amp Vout. So Vo = Vout = -4V.

For this exercise the output of the op-amp is assumed to be an ideal voltage source so it can source or sink infinite current.

You can work out the actual current the opamp is sinking or sourcing (Iout) by applying KCL at the Vo node. I will assume +ve is current flowing out of the Vo node (Note I said "out of the Vo node" not "out of the Op-Amp").

1) out of the node through the 50k load resistor... Iload = (Vo-Vgnd)/50k = Vo/50k
2) out of the node through the 100k feedback resistor... If = (Vo - Vb)/100k
3) out of the node into the Op-amp = Iout

Apply KCL...

Iout + Vo/50K + (Vo - Vb)/100K = 0

Iout = -Vo/50k - (Vo - Vb)/100k

= -Vo/50k - Vo/100k + Vb/100k

= -3Vo/100K + Vb/100K

= 12/100 + 1/100K
= 13/100K
= 0.13mA

Remember I said +ve means out of the Vo node so this means the Op-Amp is sinking current.

This is sort of what you might expect because Vo is "below ground". eg Current is flowing from Gnd through the 50k and into the op-amp output which is at -4V. eg Iload is also negative.

Edit: in case that's confusing, this shows how I applied KCL at the Vo node..

 

[Color_of_Cyan]

Could I just also use I = V/R to find the "output" current too then?Also, are you saying that you only worry about current with an op amp if there is a feedback (otherwise there is never current "through" it?)?Thanks all.

 

[CWatters]

Could I just also use I = V/R to find the "output" current too then?

What do you mean by the "output current"? If you mean the current through the 50k then yes.

Iload= -4V/50K

Also, are you saying that you only worry about current with an op amp if there is a feedback (otherwise there is never current "through" it?)?

I don't really understand what you are asking. There is no current flowing from the V+ and V- inputs to the output. The output acts like an ideal voltage source that is controlled by the voltage difference between the inputs. Any current the output sources or sinks comes from the supply pins on the op-amp.