Mutaja
- 239
- 0
Homework Statement
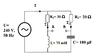
Given the circuit above.
a) Find I1, I2 and I.
b) Find the power used in branch 1 and branch 2. (please correct my "translation" if it's wrong)
c) Find the resulting impedance and phase angle. (Is resulting impedance a term?)
d) Find the voltage between node A and node B.
e) How can we get the phase angle to be 0 in the circuit?
Homework Equations
The Attempt at a Solution
The question I need help with, is c). I've done both a) and b).
My impedance, ZT, which I used in order to find the currents, is 28.3Ω ∠-20.5°
What's the difference between impedance and "result" impedance? My professor said that the magnitude of the impedance will still be the same (28.3Ω), but the phase angle will be different.
The way he explained it, I'm thinking that something is affecting the impedance, with a positive phase angle. I'm thinking the answer should be around 10 degrees.
Does anyone have any input on this problem? Please let me know if you want me to post my calculations for the first two problems. I have everything written down on paper so it won't take too long.
Appreciate any feedback.