ChristinaMaria
- 10
- 0
Hi! I am trying to solve problems from previous exams to prepare for my own. In this problem I am supposed to find the improper integral by substituting one of the "elements", but I don't understand how to get from one given step to the next.
Solve the integral
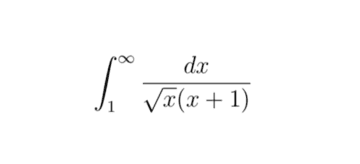
by substituting u = sqrt(x)
I don't understand how to get from step 1 to step 2:

This is one of my attempts:
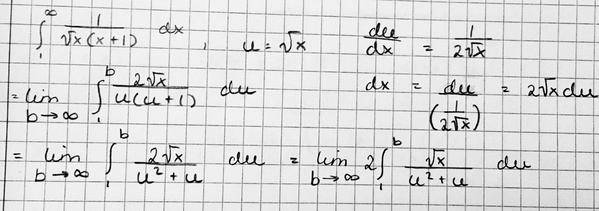
So, as I mentioned above I don't understand how to get from step one to two. I don't get what to do with the sqrt(x) you get in the expression dx = 2sqrt(x)du that I've written in the right corner. Where did it "go" in the step-by-step example? I can't seem to figure out how to remove it.
I hope this was easy enough to read.
Thanks
Homework Statement
Solve the integral
by substituting u = sqrt(x)
Homework Equations
I don't understand how to get from step 1 to step 2:
The Attempt at a Solution
This is one of my attempts:
So, as I mentioned above I don't understand how to get from step one to two. I don't get what to do with the sqrt(x) you get in the expression dx = 2sqrt(x)du that I've written in the right corner. Where did it "go" in the step-by-step example? I can't seem to figure out how to remove it.
I hope this was easy enough to read.
Thanks