How Is Final Velocity Calculated from Impulse?

AI Thread Summary
The discussion focuses on calculating the final velocity of a 538 g object acted upon by a force, with an impulse of 7 N s. The formula used is I = m∆v, where the impulse is set equal to the mass times the change in velocity. One participant initially calculated the final velocity as 13.011 m/s but received incorrect feedback. Another participant confirmed the calculation process but suggested that the issue might be related to formatting the answer without units. Ultimately, the original poster resolved their confusion with assistance from others in the thread.
AdnamaLeigh
Messages
42
Reaction score
0
The force shown in the force-time diagram acts on a 538 g object. Find the final velocity of the object if it is initially at rest. Answer in m/s.
diagram.jpg

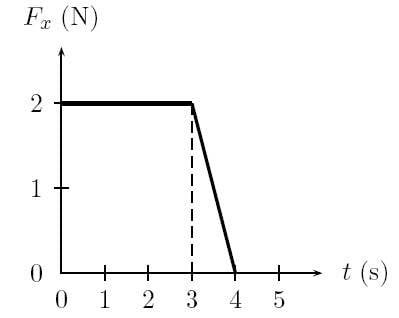
I correctly found the impulse by determining the area underneath the curve. It's 7 N s. I know that we can determine the final velocity by using this equation: I=m∆v. I also saw a topic somewhere on this site where someone suggested the same formula. I used this formula and I get the wrong answer.
7 = .583(vf - 0) vf = 13.011m/s
I also tried inputting -13.011m/s and that was also incorrect. I don't know where I'm going wrong.
 
Physics news on Phys.org
Hmm, I can't see what you've done wrong. I get the exact same answer !
 
so you get 7=.583vf? then you just divide and get 12.0007 right? or am i missing something. at any rate. is this an online problem? because if it tells you to give velocity in m/s you don't have to write the units in your submitted answer... usually. did you try that?
 
My dyslexia always seems to kick in at the worst moments. I got it. Thanks guys.
 

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...
View full post »
Thread 'Variable mass system : water sprayed into a moving container'

Thread 'Variable mass system : water sprayed into a moving container'

Starting with the mass considerations #m(t)# is mass of water #M_{c}# mass of container and #M(t)# mass of total system $$M(t) = M_{C} + m(t)$$ $$\Rightarrow \frac{dM(t)}{dt} = \frac{dm(t)}{dt}$$ $$P_i = Mv + u \, dm$$ $$P_f = (M + dm)(v + dv)$$ $$\Delta P = M \, dv + (v - u) \, dm$$ $$F = \frac{dP}{dt} = M \frac{dv}{dt} + (v - u) \frac{dm}{dt}$$ $$F = u \frac{dm}{dt} = \rho A u^2$$ from conservation of momentum , the cannon recoils with the same force which it applies. $$\quad \frac{dm}{dt}...
View full post »

Similar threads

Final velocity involving a can of soup and an inclined plane
Replies
14
Views
2K
Trying to Calculate Initial Velocity and Final Velocity
Replies
2
Views
725
Final Velocity of a car with a opposing decreasing drag force
2
Replies
57
Views
2K
1-D Motion, calculating final velocity
Replies
2
Views
1K
Calculate the Acceleration of this Car
Replies
7
Views
985
Collision finding final velocity
Replies
1
Views
1K
Golf club 🏌️and ball ⛳ impulse problem
Replies
19
Views
2K
Max Impulse on a pendulum
Replies
1
Views
812
How Do You Solve for Final Velocities in Elastic Collisions?
Replies
20
Views
2K
How Does Impulse Relate to Momentum Change in Physics Problems?
Replies
7
Views
2K

Hot Threads

Recent Insights

Back
Top