Jared944
- 10
- 0
Ok, so this problem is kind of complicated, so ask me if you need clarification. This problem deals with Impulse and Momentum.
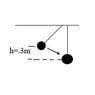
There are two balls hanging vertically from a horizontal plane. Ball A is pulled back and is set up to strike ball B.
Given for ball A -
mass = 1.5 kg.
Height = .3 m (measured from a horizontal plane from Ball B)
initial speed = 5.00 m/s (as it leaves your hand)
Given for Ball B -
mass = 4.60 kg
speed = 0 m/s (implied)
Question a) is -
Using the principle of conservation of mechanical energy, find the speed of Ball A just before impact.
Question b) is -
Assuming an elastic collision, find the velocities (magnitude and direction) of both balls just after the collision.
I can't quite set up part A, I know I have to integrate a kinematics equation and the principle of conservation of mechanical energy, but I can't quite get it right.
Thanks!
There are two balls hanging vertically from a horizontal plane. Ball A is pulled back and is set up to strike ball B.
Given for ball A -
mass = 1.5 kg.
Height = .3 m (measured from a horizontal plane from Ball B)
initial speed = 5.00 m/s (as it leaves your hand)
Given for Ball B -
mass = 4.60 kg
speed = 0 m/s (implied)
Question a) is -
Using the principle of conservation of mechanical energy, find the speed of Ball A just before impact.
Question b) is -
Assuming an elastic collision, find the velocities (magnitude and direction) of both balls just after the collision.
I can't quite set up part A, I know I have to integrate a kinematics equation and the principle of conservation of mechanical energy, but I can't quite get it right.
Thanks!