Morange
- 2
- 0
Hello,
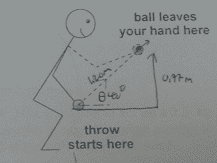
You throw a 0.500 kg rock underhand, as shown in the diagram. The rock starts at rest from the lowest point moving at an angle of 40° above the horizontal, and leaves your hand 0.300 s later having traveled 1.20 m. What is the average force that you exert on the ball while it is in your hand?
\vec{F}=\frac{∆P}{∆t}
I tried to sub the values straight in but not sure now to incorporate the force of gravity. Also I used the average speed for ∆P
F = 0.500kg*(1.2m/0.300s)/0.300s = 6.67 N
Homework Statement
You throw a 0.500 kg rock underhand, as shown in the diagram. The rock starts at rest from the lowest point moving at an angle of 40° above the horizontal, and leaves your hand 0.300 s later having traveled 1.20 m. What is the average force that you exert on the ball while it is in your hand?
Homework Equations
\vec{F}=\frac{∆P}{∆t}
The Attempt at a Solution
I tried to sub the values straight in but not sure now to incorporate the force of gravity. Also I used the average speed for ∆P
F = 0.500kg*(1.2m/0.300s)/0.300s = 6.67 N
Last edited: