Inconsistency in maxwell's equations problem.

[center o bass]

Homework Statement

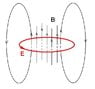
A region in space without any charges or current has a timevariable magnetic field
given by \vec{B}(t) = B_0 e^{-at} \vec{e_x} where a and B_0 are constant.

a) Use Farraday's law to show that there has to exist an electric field in this region. Find this field.

b) Show that this result is not consistent with Ampere's law. Can you explain what this result is caused by and what a correct solution would be?

Homework Equations

\oint \vec{E}\cdot \vec{dl} = -\frac{d}{dt} \int \vec{B}\cdot \vec{dA} \Leftrightarrow \nabla \times \vec{E} = - \frac{\vec{dB}}{dt}\

\oint \vec{B}\cdot \vec{dl} = \mu_0 \int \left( \vec{J} + \varepsilon_0 \frac{\vec{dE}}{dt}\right) \cdot \vec{dA} \Leftrightarrow \nabla \times \vec{B} = \mu_0 \vec{J} + \varepsilon_0 \mu_0 \frac{\vec{dE}}{dt}

The Attempt at a Solution

By Faraday's law it's easy to show that an electric field must exist in the same space by

\nabla \times \vec{E} = - \frac{\vec{dB}}{dt} = aB_0e^{-at} \vec{e_x},

but how would I go about finding the electric field when the region of space where the magnetic field is confined to isn't specified?

I would think I would need some kind of symmetry arguments to find and solve for the E-field via the integral version of Faraday's law.

Further more since it's a region of space with no charges and current. The equations reduces to

\oint \vec{E}\cdot \vec{dl} = -\frac{d}{dt} \int \vec{B}\cdot \vec{dA} \Leftrightarrow \nabla \times \vec{E} = - \frac{\vec{dB}}{dt}\

where we have this one being diffrent from zero, that is we have an induced electric field
and

\oint \vec{B}\cdot \vec{dl} = \mu_0 \int \left\varepsilon_0 \frac{\vec{dE}}{dt} \cdot \vec{dA} \Leftrightarrow \nabla \times \vec{B} = \mu_0 \varepsilon_0 \frac{\vec{dE}}{dt}.

My guess of what the inconsitency might be is that the curl of B is zero. Therefore we have

\frac{\vec{dE}}{dt} = 0, \ \ \ \nabla \times \vec{E} = - \frac{\vec{dB}}{dt} = aB_0e^{-at} \vec{e_x}

but then since the magnetic field changes with time, then curlE changes with time and therefore E must change with time. But from dE/dt = 0, this implies that E should be constant.

Have I here found the inconsistency? How could I go about explaining this result?

 

[hikaru1221]

a/ The E-field isn't specified too due to the inconsistency. But if the problem is understood as an approximate model where cylindrical symmetry exists, this can be solved by using integration form of Faraday's law. See the picture. The region where B-field is the same at every points is local. From a bigger extent, it cannot be. That's why it's approximate. In order to achieve such locally uniform B-field, there are many ways; it doesn't have to be spherical symmetry, but it sounds more "practical" to imagine that the setup is spherically symmetrical.

b/ I guess my picture already reveals the "secret" behind the inconsistency And you've found it too

 

[center o bass]

I don't know if I understand you correctly, but I think you've got me onto something.

As you've hinted the key is in the confinement of the magnetic field. The problem does not state a conefinement and therefore the magnetic field has the same strength, only pointed toward the x-direction at every point in space for a given time.

_Locally_, a varying magnetic field creates a curlE and the same is true if we confine the magnetic field to a syllindrical shape as in your picture. But if we imagine the same picture when the magnetic field was not confined we would find all the "loops" of E cancelling each other out.

So even tough we in a confined region will have an induced time varying electric field and we can solve for this one, this is really canceled by the neighbouring regions, so the electric field is constant = 0. So this explains the first inconsitency.

Furthermroe, referring to your picture, if we confine the region of the magnetic field, the magnetic field lines near the edges will circulate, so curlB is really nonzero and therefore this allows for a timevarying electric field :)

Have I got it? Thank you for the picture btw! A picture says more than a thousand words.

 

[hikaru1221]

_Locally_, a varying magnetic field creates a curlE and the same is true if we confine the magnetic field to a syllindrical shape as in your picture. But if we imagine the same picture when the magnetic field was not confined we would find all the "loops" of E cancelling each other out.

Yup. Since the uniform B-field is assumed to spread out infinitely, each point in the space can be viewed as a center of such cylindrical symmetry (oops, I've just read my post again and saw that I wrote it wrongly it should be "cylindrical symmetry", not "spherical symmetry" ), and again, as the uniform B-field spreads infinitely, E-fields due to each couple of centers that are opposite each other through a point P cancel out. The result is E-field at P = 0. But again, Faraday's law shows that E-field cannot be zero.

However the inconsistency is due to the assumption that such magnetic field can exist. In fact, it should look like something in my picture, right? This is because B-field line never ends! It has to be a closed curve. Even if there is a magnet here, it cannot be infinitely big. That means, the assumption conflicts with the nature of B-field, while Maxwell's equations (including Faraday's law and Ampere's law) concur with that nature. So the inconsistency is not so surprising.

It can easily be seen that in a cylindrically symmetrical setup, the center has E-field = 0. This is consistent with the above argument based on symmetry. Other points do not have such symmetry, so E-field is not 0.