Increasing counterclockwise number of integers

In summary, the task is to find the sum of the numbers directly above and below the number 2008 in a counterclockwise spiral of infinite integers starting with 1. The key is to find patterns in the numbers and use them to locate 2008 on the spiral. One suggested strategy is to identify which arm of the spiral 2008 will occur in, then determine its position within that arm, and finally work out the relationship between the numbers in that position and the adjacent ones. Another suggested strategy is to consider the numbers that occur at the extreme ends of the rightward spiral and look for a pattern. One example given is to solve for (2n+1)^2-k where k<n and then try different values
  • #1
hermes2014
2
0

Homework Statement


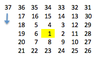
In the image below we start with the integer 1 marked in yellow. We will fill the rest of the table in counterclockwise manner with integers to infinity. What will be the sum of the numbers right above and below the number 2008?

attachment.php?attachmentid=67448&stc=1&d=1394398270.png


Homework Equations


-


The Attempt at a Solution


I think it has something to do with positive/ negative integers.
 

Attachments

  • Screen Shot 2014-03-09 at 20.16.47.png
    Screen Shot 2014-03-09 at 20.16.47.png
    2.7 KB · Views: 442
Physics news on Phys.org
  • #2
This reminds me of a project Euler problem. The key is to find patterns in the numbers, locate where that number would be, and then do a little grunt work to find the numbers above and below it. For example, the most apparent pattern to me is what happens with the numbers to the SE of 1. Draw out a 11x11 (or bigger) grid and see what you can find.
 
  • #3
scurty said:
This reminds me of a project Euler problem. The key is to find patterns in the numbers, locate where that number would be, and then do a little grunt work to find the numbers above and below it. For example, the most apparent pattern to me is what happens with the numbers to the SE of 1. Draw out a 11x11 (or bigger) grid and see what you can find.

That idea also came to my mind. There is some pattern here that I at least haven't observed yet. I've tried to map it out on a larger grid and still wasn't able to find anything.

Maybe one additional piece of information, this question was presented as part of a 45 min/ 30 question test to assess your abilities for a business game... To me it seems that there must be something obvious about this that I'm missing.
 
  • #4
Here's a strategy that might work. First find out which arm of the 'spiral' 2008 will occur in. Then figure out roughly where in the spiral (at either end or somewhere in the middle?) of that arm it will occur. Finally try to work out the relationship between numbers in the middle of one of that sort of arm with the adjacent ones.

To get you started on the first part, notice that 2, 10, 26, ... always seem to occur at the extreme ends of the 'rightward' spiral. Can you see the pattern that governs these numbers? How long are these rightward spiral arms?
 
  • #5
Answer the question for (2n+1)^2-k
k<n
then let n=22,k=17

If general k seems hard do k=1,2,..
until you see the pattern
 

FAQ: Increasing counterclockwise number of integers

1. What is meant by increasing counterclockwise number of integers?

Increasing counterclockwise number of integers refers to the arrangement of numbers in a sequence where each successive number is one less than the previous number and the sequence is read in a counterclockwise direction. For example, the sequence 10, 9, 8, 7, 6, 5, 4, 3, 2, 1 would be an increasing counterclockwise number of integers.

2. Why is it important to study increasing counterclockwise number of integers?

Studying increasing counterclockwise number of integers can help in understanding mathematical concepts such as patterns, sequences, and number relationships. It can also improve logical thinking and problem-solving skills.

3. What are some real-world applications of increasing counterclockwise number of integers?

Increasing counterclockwise number of integers can be seen in various everyday activities such as counting down a timer, playing a game of chess, or organizing items in a reverse order.

4. How can one increase the counterclockwise number of integers in a given sequence?

To increase the counterclockwise number of integers in a given sequence, simply subtract one from each number in the sequence. For example, the sequence 10, 9, 8, 7, 6 would become 9, 8, 7, 6, 5 when the counterclockwise number of integers is increased.

5. Are there any limitations to increasing counterclockwise number of integers?

Yes, there are limitations to increasing counterclockwise number of integers. The sequence cannot continue indefinitely as it would eventually reach negative numbers, which are not considered integers.

Similar threads

Finding 5 Positive Integers with GCD Difference
Replies
6
Views
2K
Proving Induction for All Integers
Replies
3
Views
1K
No Divisors Between an Integer and Twice it
Replies
3
Views
998
Prove that a^(1/n) is an integer or is irrational
Replies
7
Views
2K
Can b be an integer if it does not divide k for every natural number k?
Replies
2
Views
1K
Integers as the sum of 3 integers.
Replies
2
Views
1K
General formula for a combination of four categories
Replies
3
Views
1K
How many ways to count to 20 with positive integers and x > 3?
Replies
22
Views
2K
What Is the Product of Primes for the Integer 23?
Replies
2
Views
1K
Is there a better way to find the number of integer solutions
Replies
5
Views
2K

Hot Threads

Recent Insights

Back
Top