Induced Current Direction in a Moving Square Loop

[flyingpig]

Homework Statement

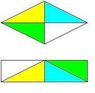
The square loop in the figure below is made of wires with a total series resistance of 10.0. It is placed in a uniform 0.100 T magnetic field directed perpendicular into the plane of the paper. The loop, which is hinged at each corner, is pulled as shown until the separation between points A and B is 3 m. If this process takes 0.100 s, what is the magnitude and direction of the average current generated in the loop?

The Attempt at a Solution

R = 10.0Ω
B = 0.100T
l = 3.00m
t = 0.100s
I = ?

\varepsilon = -\frac{\Delta \Phi_{B}}{\Delta t} = IR

So the B-field is into the page

\varepsilon = -\frac{\Delta B l^2}{\Delta t} = IR

-\frac{\Delta B l^2}{\Delta t R} = I

Now I have two questions

From this http://answers.yahoo.com/question/index?qid=20090310141926AAQd4oC

The guy took the area from sin(60), I don't understand what he is doing, isn't the area is just l²??

Also, for the direction of the current, is there a quantitative way of knowing the direction?

Judging from -\frac{\Delta B l^2}{\Delta t R} = I, the negative sign suggests it is clockwise

Is there another way of knowing the direction?

 

[flyingpig]

When they mean the distance between A and B are 3.00m apart, do they mean this instead...? I think I underestimated this problem

[PLAIN]http://img291.imageshack.us/img291/9748/p2058.gif

 

[gneill]

The figure starts as a square, then gets stretched horizontally and squeezed vertically until points A and B are 3.00 meters apart.

 

[flyingpig]

So I am wrong right lol? The geometry becomes difficult...

 

[flyingpig]

Please help, it's due tomorrow...

 

[flyingpig]

Actually if you pull it how could it become shorter?? The original distance is 3\sqrt{2}

 

[gneill]

Yes, 3√2 m is about 4.244m. What's wrong with that? It can go from there down to 3.00m.

 

[flyingpig]

OKay okay forget the theoretical part for now lol, I regret asking that question. How do I make up for the new Area? because it isn't a square anymore

 

[flyingpig]

And since the four sides changes, how do I find the area? I have only the diagonal length. Please help me! It's due tomorrow!

 

[SammyS]

OKay okay forget the theoretical part for now lol, I regret asking that question. How do I make up for the new Area? because it isn't a square anymore

Area of a rhombus?

Cut it along either diagonal into two congruent triangles. Double the area of either triangle.

 

[flyingpig]

A rhombus? I thought it was a parallelogram.

 

[flyingpig]

Also doesn't the 3.00m change too?

 

[gneill]

The side lengths stay the same. They are "hinged", so the figure can be distorted while the side lengths stay the same. The area is easy to compute given the major and minor axes lengths.

 

[flyingpig]

so I have

For the top congruent triangle I got

\frac{1.5 \cdot 2 \sqrt{3^2 - 1.5^2}}{2} = 3.897

So twice that is 7.79m²

Before I even continue I got it right right?

 

[SammyS]

A rhombus? I thought it was a parallelogram.

Look up rhombus before posting something like this.

 

[flyingpig]

Nah the key word was hinged...

 

[flyingpig]

Oh wait looks like my "theoretical" question had been answered too then lol

 

[SaraF]

I think the problem is pretty easy to solve if you recognize that the change in magnetic flux is the product of the (constant) magnetic field and the change in area.
The change in area can be calculated using basic geometry...calculate the original area, calculate the final area, and subtract original from final, divide by the time interval, and you have the average EMF. I don't know how to get equations into the post, so I can't demonstrate. As for the direction of the current induced, since you are decreasing the area enclosed in the wire you are also decreasing the flux pointing into the page...by Lenz's law the induced current would be in the direction that increases flux pointing into the page...use the right-hand rule for that.
Good luck.