Jahnavi
- 848
- 102
Homework Statement
Homework Equations
The Attempt at a Solution
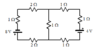
Sorry for the unclear image .
EMF induced in the left loop = 8
Total Resistance of the left loop = 6 Ohms
Current will be induced in anticlockwise direction in the left loop of magnitude 4/3A.
EMF induced in the right loop = 4
Total Resistance of the left loop = 4 Ohms
Current will be induced in anticlockwise direction in the right loop of magnitude 1 A.
By superposing the two currents , current flowing in the middle branch is 1/3 Ohms from bottom to top .
But the answer given is different .
Am I making some mistake ?