- #1
dascribe
- 3
- 0
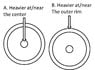
If I make 2 wheels of identical size and weight, so that the only difference bewteen the 2 is that wheel A has most of its weight at the center of the wheel and wheel B has most of its weight equally distributed on the circumference of the wheel:
1. Which wheel would spin longer if both wheels were initially spun with equal force?
2. Would one wheel spin faster than the other given the same force?
***The wheel is placed horizontally like a top
thanks
1. Which wheel would spin longer if both wheels were initially spun with equal force?
2. Would one wheel spin faster than the other given the same force?
***The wheel is placed horizontally like a top
thanks