Homework Help Overview
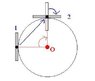
The problem involves a uniform rod of length l that is subjected to an impulse at right angles to its length, with the goal of determining the distance of the instantaneous center of rotation from the center of the rod. The discussion centers around concepts of impulse, momentum, and angular momentum in the context of rotational motion.
Discussion Character
- Exploratory, Conceptual clarification, Mathematical reasoning
Approaches and Questions Raised
- Participants discuss the relationship between impulse and momentum, questioning the correct formulation of initial angular momentum. There is also exploration of how torque relates to angular momentum and the implications of the instantaneous axis of rotation.
Discussion Status
Some participants have provided insights into the relationships between torque, impulse, and angular momentum. There is an ongoing exploration of the concept of "pure rotation" and how it applies to the motion of the rod. Multiple interpretations of the instantaneous axis are being considered.
Contextual Notes
Participants are navigating through the definitions and implications of impulse and torque, as well as the assumptions regarding the motion of the rod. There is a focus on understanding the dynamics of the system without reaching a definitive conclusion.
