Karol
- 1,380
- 22
Whats's the volume under the revolving parabola y=ax2. R is xmax.
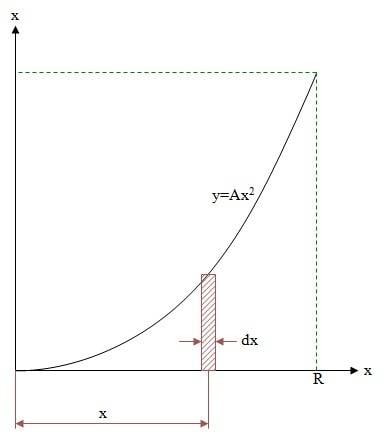
$$V=\int_0^R\pi xdx\cdot y=\pi\int_o^R x\cdot Ax^2dx=\pi A\frac{R^4}{4}$$
Volume should be relative to R3. and if i had, for example, y=Ax3 then, according to my calculation i would get relative to R7 and so on.
$$V=\int_0^R\pi xdx\cdot y=\pi\int_o^R x\cdot Ax^2dx=\pi A\frac{R^4}{4}$$
Volume should be relative to R3. and if i had, for example, y=Ax3 then, according to my calculation i would get relative to R7 and so on.