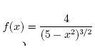You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Integrate Function: Can't Find Answer Key - Help Needed
- Thread starter okevino
- Start date
-
- Tags
- Integrate
Physics news on Phys.org
Mute
Homework Helper
- 1,388
- 12
Have you learned trigonometric substitution? Let x = \sqrt(5)\sin\theta, and use the pythagorean identity to write 5(1-\sin^2\theta) = 5\cos^2\theta.
Under this change of variables, dx = \sqrt(5)\cos\theta d\theta. Your integral then becomes an integral over a constant times 1/\cos^2\theta = sec^2\theta. If you know the integral of sec^2\theta, you're pretty much done then.
Under this change of variables, dx = \sqrt(5)\cos\theta d\theta. Your integral then becomes an integral over a constant times 1/\cos^2\theta = sec^2\theta. If you know the integral of sec^2\theta, you're pretty much done then.
okevino
- 13
- 0
alright..
but where did the 3/2 go..
but where did the 3/2 go..
okevino
- 13
- 0
right now i have...
4/5 integral sec^2 theta..
if I'm right at this point
so...
integral of sec^2 is tan x
but i set x = root5 sin theta earlier..
how do i finish this question..
4/5 integral sec^2 theta..
if I'm right at this point
so...
integral of sec^2 is tan x
but i set x = root5 sin theta earlier..
how do i finish this question..
Last edited:
Gib Z
Homework Helper
- 3,341
- 7
The Exponents canceled each other out.
\int \frac{4}{(5-x^2)^{3/2}} dx.
Now We do the substitution Mute said. dx = \sqrt(5)\cos\theta d\theta
So now the integral is \int {4\sqrt{5} \cos \theta}{5^{3/2}\cdot (\cos^2 \theta)^{3/2}} d\theta
We can take all constants out. When we have a power to a power, we multiply the powers. 3/2 times 2 is just 3.
\frac{4\sqrt{5}}{5^{3/2}} \int \frac{\cos \theta}{\cos^3 \theta} d\theta = \frac{4\sqrt{5}}{5^{3/2}} \int \frac{1}{\cos^2 \theta} d\theta. As Mute said, 1/cos^2 theta is sec^2 theta. And the integral of that is easy, you should know that.
\int \frac{4}{(5-x^2)^{3/2}} dx.
Now We do the substitution Mute said. dx = \sqrt(5)\cos\theta d\theta
So now the integral is \int {4\sqrt{5} \cos \theta}{5^{3/2}\cdot (\cos^2 \theta)^{3/2}} d\theta
We can take all constants out. When we have a power to a power, we multiply the powers. 3/2 times 2 is just 3.
\frac{4\sqrt{5}}{5^{3/2}} \int \frac{\cos \theta}{\cos^3 \theta} d\theta = \frac{4\sqrt{5}}{5^{3/2}} \int \frac{1}{\cos^2 \theta} d\theta. As Mute said, 1/cos^2 theta is sec^2 theta. And the integral of that is easy, you should know that.
Gib Z
Homework Helper
- 3,341
- 7
O and the constant on the outside simplifies to 4/5.
okevino
- 13
- 0
that's exactly what i said ..
but if i take the integral from 1 to 2..
i dont' get the answer 6/5
cuz i think if you set x to some value.
the upper and lower bound needs to change..
but i dont' remember if there's such thing..
but if i take the integral from 1 to 2..
i dont' get the answer 6/5
cuz i think if you set x to some value.
the upper and lower bound needs to change..
but i dont' remember if there's such thing..
Gib Z
Homework Helper
- 3,341
- 7
Well The integral is (4/5) tan theta.
x = sqrt{5} sin theta.
sin theta = x/(sqrt5)
theta = arcsin (x/sqrt5)
The integral is therefore 4/5 tan (arcsin x/sqrt5). Plug in x values and subtract.
x = sqrt{5} sin theta.
sin theta = x/(sqrt5)
theta = arcsin (x/sqrt5)
The integral is therefore 4/5 tan (arcsin x/sqrt5). Plug in x values and subtract.
okevino
- 13
- 0
my x values are 1 to 2..
if i sub into arcsinx it's undefined.
if i sub into arcsinx it's undefined.
Mute
Homework Helper
- 1,388
- 12
That would be a problem, except that you want to sub into arcsin(x/sqrt5), not arcsinx.
okevino
- 13
- 0
wow...
great...
got it...
thanks mute and GibZ..
great...
got it...
thanks mute and GibZ..
Similar threads
- Replies
- 5
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 7
- Views
- 2K
- Replies
- 3
- Views
- 2K
- Replies
- 8
- Views
- 2K
- Replies
- 3
- Views
- 1K
- Replies
- 5
- Views
- 2K
- Replies
- 2
- Views
- 3K
- Replies
- 3
- Views
- 1K
- Replies
- 7
- Views
- 2K
Hot Threads
-
I Harmonic series Ʃ1/n diverges but p-series Ʃ(1/n)^p diverges?
- Started by Dimwitted_UniStudent
- Replies: 4
- Calculus
Recent Insights
-
Insights Quantum Entanglement is a Kinematic Fact, not a Dynamical Effect
- Started by Greg Bernhardt
- Replies: 7
- Quantum Physics
-
Insights What Exactly is Dirac’s Delta Function? - Insight
- Started by Greg Bernhardt
- Replies: 0
- General Math
-
Insights Relativator (Circular Slide-Rule): Simulated with Desmos - Insight
- Started by Greg Bernhardt
- Replies: 1
- Special and General Relativity
-
Insights Fixing Things Which Can Go Wrong With Complex Numbers
- Started by PAllen
- Replies: 7
- General Math
-
Insights Fermat's Last Theorem
- Started by fresh_42
- Replies: 91
- General Math
-
Insights Why Vector Spaces Explain The World: A Historical Perspective
- Started by fresh_42
- Replies: 0
- General Math