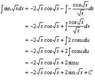Can you integrate sin(sqrt(x)) using a trigonometric substitution?

[Alkatran]

I need to know how to integrate this function:
sin(sqrt(x))
I did this:
u = sqrt(x)
du/dx = 1/(2sqrt(x))

S(sin(sqrt(x))dx) = S(sin(u)*dx*du/dx/(2sqrt(x)) = S(Sin(u)/u du)

But then I got stuck: integration by parts won't work, trig substitution is out...

The one thing I did come up with was:
(u/v)' = (u'v - uv')/v^2
S((u/v)') = uv = S((u'v - uv')/v^2)

So I changed
S(sin(u)/u)
to
S(sin(u)*u/u^2 + cos(u)/u^2 - cos(u)/u^2)
= S((sin(u)*u + cos(u))/u^2) - S(cos(u)/u^2)
= cos(u)/u - S(cos(u)/u^2)

But I get the feeling I'm barking up the wrong tree. If I do integration by parts on that integral I'm going to end up with sin(u)/u again! :grumpy:

 

[Hurkyl]

Are you sure you need an elementary formula for the integral? Getting, say, a Taylor series for an antiderivative would be fairly straightforward, as would estimating a definite integral with numerical approximation.

 

[dextercioby]

$$Si(x)=:\int_{0}^{x} \frac{\sin t}{t} dt$$

is called SINE INTEGRAL and is not an "elementary" function.

Daniel.

 

[houserichichi]

I apologize, I have no desire to write out the latex code...it's much too late for that :yuck:

 

[dextercioby]

Well,Alkatran,your initial substitution was good,unfortunately you got lost on the way.

$$\int \sin\sqrt{x} \ dx =...??$$

Make the substitution:
$$\sqrt{x}=u$$ equivalently:
$$x=u^{2}$$

Can u take it from here?

Daniel.

 

[Alkatran]

Well,Alkatran,your initial substitution was good,unfortunately you got lost on the way.

$$\int \sin\sqrt{x} \ dx =...??$$

Make the substitution:
$$\sqrt{x}=u$$ equivalently:
$$x=u^{2}$$

Can u take it from here?

Daniel.

I don't see how $$x=u^{2}$$ helps? There are no x's in the equation. However...

$$\int \sin\sqrt{x} \ dx = \int {\sin\sqrt{u^{2}}}/u \ du$$
$$\sin\sqrt(u)^{2} = {1 - \cos{2*\sqrt{u}}}/2$$

But I get the feeling I'm headed for circles again.

We haven't covered integral approximation or taylor series yet so I would have no idea how to do that. However, the initial problem was slightly simpler: It had upper and lower limits (and I believe the answer involved pi).



On another note:
A small question: I was given a question once with the hint: this is the area of a common shape...

Well I realized it was a circle, and did the question without even using integration, but I was just wondering how I would integrate a circle's function (well, top half of a circle's function)?

 

[dextercioby]

$$x=u^{2} \Rightarrow dx=2u \ du$$

Write the integral in terms of "u".

Daniel.

 

[robert Ihnot]

Maybe what is missing is the idea of Intergation by Parts:

$$\int{ysin(y)dy}=-ycos(y) + \int{cos(y)dy}$$


To integrate the circle function (X^2+Y^2 =R^2 in the first quadrant, we solve for Y= $$\sqrt{R^2-X^2}$$ and then to solve for X=0 to 1, we will require a trigonometric substitution. (This occurs because pi is a transcendental function and can not be obtained from a finite polynomial.)