zachem62
- 37
- 3
Homework Statement
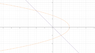
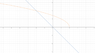
Find the area of the region enclosed by x=2-y2 and x+y=0 integrating with respect to y.
Homework Equations
The Attempt at a Solution
this confuses me because when integrating with respect to y, you get the functions in terms of x and then integrate them as you would. but when you do that, there is no enclosed area. what i mean is when you have y=√(2-x2) and y=-x, there is an intersection at x=-1 but that's it...so there is no enclosement and i don't know how to integrate here...please help!
thanks.