- #1
Adel Makram
- 635
- 15
Missing homework template due to originally being posted in other forum.
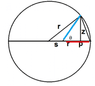
I am interested to find the length shown in red in the attached figure. I want this length as a function of d (shown in blue) and the angle θ. Then I will integrate this length to dθ from 0 to π/2.
Firstly, I used the law of the triangle to determine the length s which when subtracted from the radius r yields the desired length p.
s2+2sd cosθ+ d2-r2=0
Then I used a substitute a2=d2/ r2-d2
which gives, -sqrt(r2-d2 ∫ sqrt {(a2 cos2(θ)-1} dθ
Lastly, I used wolframe alfa to calculate the part under integration, here is what I got.( I used r=1 and d=1/2 r).
The result is a complex number ( attached). I don`t understand how the integration of a length which is a real number results into a complex number.
Firstly, I used the law of the triangle to determine the length s which when subtracted from the radius r yields the desired length p.
s2+2sd cosθ+ d2-r2=0
Then I used a substitute a2=d2/ r2-d2
which gives, -sqrt(r2-d2 ∫ sqrt {(a2 cos2(θ)-1} dθ
Lastly, I used wolframe alfa to calculate the part under integration, here is what I got.( I used r=1 and d=1/2 r).
The result is a complex number ( attached). I don`t understand how the integration of a length which is a real number results into a complex number.
Attachments
Last edited: