- #1
chwala
Gold Member
- 2,650
- 351
- Homework Statement
- See attached.
- Relevant Equations
- Complex Numbers
Hello guys,
I am refreshing on complex numbers today; kindly see attached.
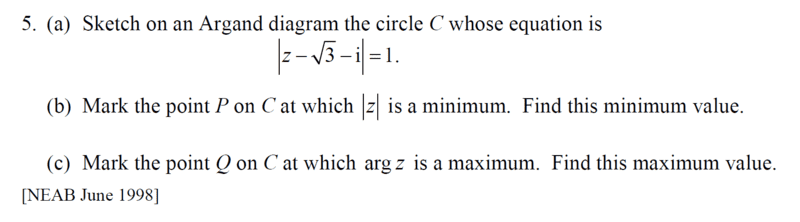
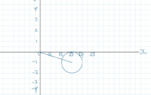
ok for part (a) this is a circle with centre ##(\sqrt{3}, -1)## with radius =##1## thus, we shall have,

I am refreshing on complex numbers today; kindly see attached.
ok for part (a) this is a circle with centre ##(\sqrt{3}, -1)## with radius =##1## thus, we shall have,