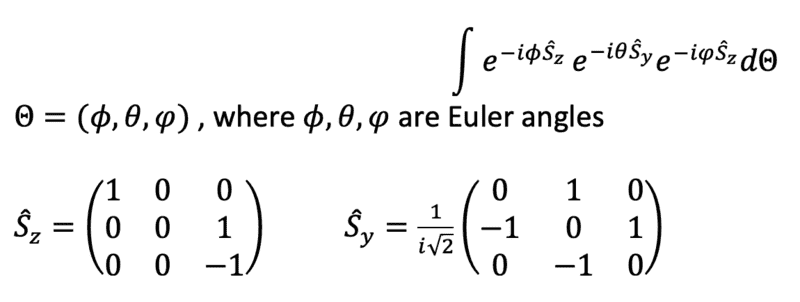RiceSweet
- 5
- 2
Hello, I was struggling with solving a specific integral. I know that I can rewrite the exponential matrices and the range of the three Euler angles. However, I am not sure I should I write
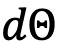 in terms those three Euler angles.
in terms those three Euler angles.