- #1
barnflakes
- 156
- 4
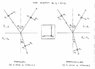
Please see the diagram attached, I don't understand how my lecturer is resolving the E-field in the perpendicular case.
He obtains:
[tex]E_i = \bold{y} e^{-i\omega(t - \frac{n_1}{c} (-xsin \theta_i - z cos \theta_i))}[/tex]
How has he obtained the [tex](-xsin \theta_i - z cos \theta_i)[/tex] part from that diagram? What are x and z in that expression? As far as I can see, the E field is perpendicular to the plane of incidence so why does it have those components? Just to reiterate I'm talking about the E field being polarised perpendicular to the plane, so the right hand diagram.
Cheers guys.
He obtains:
[tex]E_i = \bold{y} e^{-i\omega(t - \frac{n_1}{c} (-xsin \theta_i - z cos \theta_i))}[/tex]
How has he obtained the [tex](-xsin \theta_i - z cos \theta_i)[/tex] part from that diagram? What are x and z in that expression? As far as I can see, the E field is perpendicular to the plane of incidence so why does it have those components? Just to reiterate I'm talking about the E field being polarised perpendicular to the plane, so the right hand diagram.
Cheers guys.