physicsfox
- 11
- 0
Here’s a question for you all… but first some background
(see jpeg attachment for sketch)
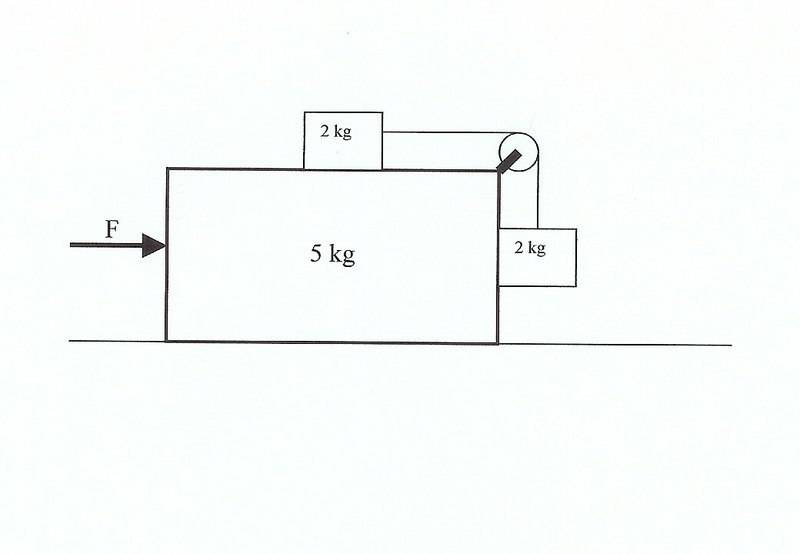
Assuming all surfaces are frictionless (5kg on horizontal surface, two 2kg blocks on 5kg block), and the pulley has no mass, with what horizontal force applied to the 5kg block will the two 2kg blocks remain in the same location relative to 5kg block? In other words, with what applied force, F, will the two 2kg blocks remains “fixed” against the 5kg block (relative acceleration 0)?
If the vertically hanging 2kg block is to remain at the same vertical position as the system accelerates to the right, then the tension above the hanging 2kg block will be equal to the Fg of the hanging 2 kg block. The Tension is 20N. The horizontal 2kg block is therefore being pulled to the right by the same T=20N. The acceleration of the 2kg block is then 10 m/s2 (F=ma). To create that 20N in the horizontal string, the system needs to accelerate at 10m/s2. Thus, F=90N. (F=ma=9kg*10m/s2).
Now the question. Assuming the above is correct, what would happen if the applied horizontal force was, let’s say, 100N? Qualitatively, the two 2kg blocks would not remain at the same position relative to the 5kg block. The horizontal 2kg block would move towards the back of the 5kg block, and the vertical 2 kg block would rise up. Would the two blocks have a relative acceleration? I would think so. But how would you quantify this acceleration? How would you quantify the acceleration of the 5kg block? Is the 100N pushing the entire mass (9kg), or does the relative acceleration of the two 2kg blocks have some affect that I am not considering?
I would appreciate any thoughts on this.
(see jpeg attachment for sketch)
Assuming all surfaces are frictionless (5kg on horizontal surface, two 2kg blocks on 5kg block), and the pulley has no mass, with what horizontal force applied to the 5kg block will the two 2kg blocks remain in the same location relative to 5kg block? In other words, with what applied force, F, will the two 2kg blocks remains “fixed” against the 5kg block (relative acceleration 0)?
If the vertically hanging 2kg block is to remain at the same vertical position as the system accelerates to the right, then the tension above the hanging 2kg block will be equal to the Fg of the hanging 2 kg block. The Tension is 20N. The horizontal 2kg block is therefore being pulled to the right by the same T=20N. The acceleration of the 2kg block is then 10 m/s2 (F=ma). To create that 20N in the horizontal string, the system needs to accelerate at 10m/s2. Thus, F=90N. (F=ma=9kg*10m/s2).
Now the question. Assuming the above is correct, what would happen if the applied horizontal force was, let’s say, 100N? Qualitatively, the two 2kg blocks would not remain at the same position relative to the 5kg block. The horizontal 2kg block would move towards the back of the 5kg block, and the vertical 2 kg block would rise up. Would the two blocks have a relative acceleration? I would think so. But how would you quantify this acceleration? How would you quantify the acceleration of the 5kg block? Is the 100N pushing the entire mass (9kg), or does the relative acceleration of the two 2kg blocks have some affect that I am not considering?
I would appreciate any thoughts on this.