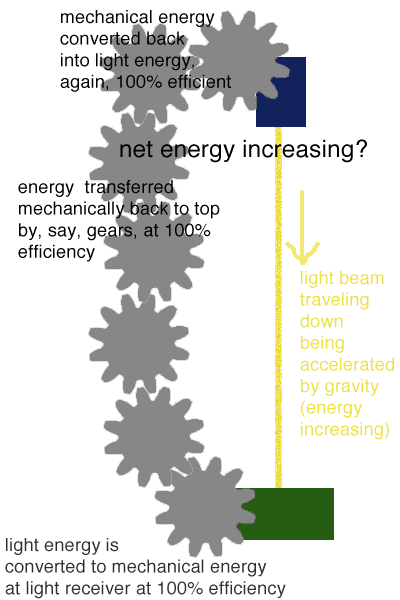
This makes some sense to me, but:
(1) Let the difference in gravitational potential between the top and bottom of the apparatus be ΔΦ, so that time dilation gives t'=kt, where k=1+ΔΦ (with c=1). It seems to me that the kinetic energy of the gears would scale by k
2, whereas the energy of the photons only scales by k.
(2) I don't think it really works to invoke locality. If you just use a single big gear, clearly "local" isn't big enough to include both the top and the bottom of the gear. This is why I'm guessing that it's not possible to have the gears be rigid to the approximation required for transmission of energy that is lossless compared to the energy gained by the photons on the way down.
Here are a couple of references on the generalization of rigidity from SR to GR:
F.A.E. Pirani and Gareth Williams, "Rigid motion in a gravitational field," Séminaire Janet. Mécanique analytique et mécanique céleste, tome 5, (1961-1962), exp. no 8-9, p. 1-16, available for free at permanent url
http://www.numdam.org/item?id=SJ_1961-1962__5__A8_0
Boyer, Rigid Frames in General Relativity, Proc. R. Soc. Lond. A 19 January 1965 vol. 283 no. 1394 343-355
I don't have access to the second one.