- #1
aranud
- 20
- 0
Homework Statement
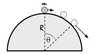
This week’s physics puzzle is a classic often used in mechanics. A point-like marble of mass m is situated on top of an immobile hemisphere of radius R. It is given a tiny push and starts rolling down. At what angle θ will it detach from the hemisphere’s surface and fly off? Assume there is no friction between the marble and the hemisphere, and treat the marble as a point object.
Homework Equations
v^2/r=centripetal acceleration=omega^2*r
omega*r=circumferential speed
The Attempt at a Solution
This is just an interesting problem i saw at a blog. A solution had been given but the link is broken now. I haven't been able to find the answer and i would really like your thoughts on it.Here's what I've come up with, i should however tell you that i am not very skilled at calculus, never having had any formal education in it.
I think the angle the ball makes with the hemisphere is 90°-theta
So the gravitational acceleration can be taken apart as a
tangential acceleration:g*cos(90°-theta) =g*sin(theta)
and a
normal acceleration:g*sin(90°-theta) =g*cos(theta)
(which i think serves as a centripetal acceleration here)
if integrate the tangential acceleration to get the speed i get: -g*cos(theta)
which surprises me because it's negative (have i already made a mistake?)
Now i think that a at some angle theta the speed will be so large that the centripetal acceleration can't hold it anymore and it flies off. So all that is left for me to do is to find a way to compare the centripetal acceleration i would i expect with a given speed to the centripetal acceleration i actually have. The moment that the expected centripetal acceleration is larger than the given, i now that is the angle theta the ball will fly off.
I'm guessing i'll have to use the expressions omega*r and omega^2*r to compare them but i don't immediately see how.
Thanks ( and if I'm on the right track just a hint will do :) )
 "Centrifugal force" is only used when describing things from an accelerated reference frame; forget about it.
"Centrifugal force" is only used when describing things from an accelerated reference frame; forget about it.